题目内容
【题目】已知二次函数![]() ,设
,设![]() 是函数
是函数![]() 在
在![]() 上的最大值.
上的最大值.
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的解析式;
的解析式;
(2)若对任意的![]() ,恒有
,恒有![]() ,求满足条件的所有实数对
,求满足条件的所有实数对![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:本题表面上是新定义问题,实质上新定义仅仅是最大值的另一种说法,(1)问题就是求![]() 在区间
在区间![]() 上的最大值,由于绝对值符号里面的式子
上的最大值,由于绝对值符号里面的式子![]() 是二次的,对称轴是
是二次的,对称轴是![]() ,因此其在区间
,因此其在区间![]() 上递减,从而只要考虑
上递减,从而只要考虑![]() 和
和![]() 的大小可得结论;(2)首先要求
的大小可得结论;(2)首先要求![]() ,从(1)的研究知,须按
,从(1)的研究知,须按![]() 对称轴与区间的关系分类,当
对称轴与区间的关系分类,当![]() 或
或![]() 时,
时,![]() 在区间
在区间![]() 上单调,因此有
上单调,因此有![]() ,
,![]() ,下面对此式进行放缩,有
,下面对此式进行放缩,有![]()
![]()
![]()
![]() ,研究这里三个不等号取等号的条件可得
,研究这里三个不等号取等号的条件可得![]() ,当
,当![]() 时,还需分类讨论到底有
时,还需分类讨论到底有![]() 还是有
还是有![]() ,(按
,(按![]() 的大小分类,也即1,2哪个离对称轴远),同上进行放缩以求得取最小值时的
的大小分类,也即1,2哪个离对称轴远),同上进行放缩以求得取最小值时的![]() ,比较
,比较![]() 的最小值可得
的最小值可得![]() .
.
试题解析:(1)当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递减,故
上单调递减,故![]() 在
在![]() 上的值域为
上的值域为![]() .
.
从而![]() ;
;
(2)函数![]() 的对称轴为
的对称轴为![]() ,下面讨论
,下面讨论![]() 的大小关系来确定
的大小关系来确定![]() 的单调性.
的单调性.
①当![]() 或
或![]() 时,
时,![]() 在
在![]() 上单调,又
上单调,又![]() ,
,![]() ,
,
![]()
![]()
不等号1,2,3取到等号的条件分别为 或
或 ,
,
从而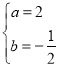 或
或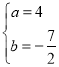
②当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,又
上单调递减,又![]() ,
,
![]() ,
,![]()
ⅰ)当![]() 时,
时,![]()
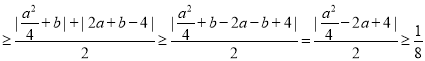
不等号1,2,3取到等号的条件分别为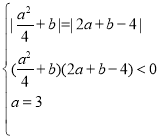 ,故
,故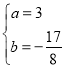 .
.
ⅱ)当![]() 时,
时,![]()
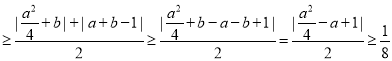
不等号1,2,3取到等号的条件分别为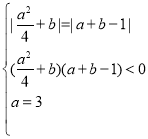 ,故
,故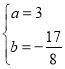 ,这与
,这与![]() 矛盾.
矛盾.
综上所述,当且仅当![]() ,
,![]() 时,对任意的
时,对任意的![]() ,恒有
,恒有![]() ,
,
故满足条件的所有实数对![]() 为
为![]() .
.

练习册系列答案
相关题目
【题目】某中学调查了某班全部45名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 | 8 | 5 |
未参加演讲社团 | 2 | 30 |
(I)从该班随机选1名同学,求该同学至少参加上述一个社团的概率;
(II) 在既参加书法社团又参加演讲社团的8名同学中,有5名男同学![]() ,3名女同学
,3名女同学![]() ,现从这5名男同学和3名女同学中各随机选1人,求
,现从这5名男同学和3名女同学中各随机选1人,求![]() 被选中且
被选中且![]() 未被选中的概率。
未被选中的概率。