题目内容

如图，矩形ABCD中PD⊥平面ABCD，若PB=2，PB与平面ABCD成30°角，PB与平面PCD成45°角，求：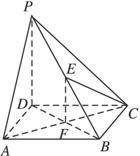

（1）CD的长；

（2）求PB与CD所成?的角.

解析：（1）∵PD⊥平面ABCD∴∠PBD是PB与平面ABCD所成的角.

∵PD⊥平面ABCD.BC面ABCD，

∴PD⊥BC.又BC⊥CD，PD∩CD=D，

∴BC⊥面PCD.

则∠BPC是PB与平面PCD所成的角,

∠PBD=30°，PB=2，∠BPC=45°.

PC=BC=,PD=1，∴DC=1.

（2）PA=,AB=1,PB=2.

∠PBA=60°，即为PB与CD所成角.


练习册系列答案
相关题目
精英家教网如图，矩形ABCD中，AB=
8
3
3
，BC=2，椭圆M的中心和准线分别是已知矩形的中心和一组对边所在直线，矩形的另一组对边间的距离为椭圆的短轴长，椭圆M的离心率大于0.7．
（I）建立适当的平面直角坐标系，求椭圆M的方程；
（II）过椭圆M的中心作直线l与椭圆交于P，Q两点，设椭圆的右焦点为F2，当∠PF2Q=
2π
3
时，求△PF2Q的面积．
如图，矩形ABCD中，AB=1，AD=2，M为AD的中点，则
BM
•
BD
的值为
 
．
精英家教网
A 若方程ax-x-a=0有两个实数解，则a的取值范围是
（1，+∞）
（1，+∞）

B 如图，矩形ABCD中边长AB=2，BC=1，E为BC的中点，若F为正方形内（含边界）任意一点，则
AE
•
AF
的最大值为
9
2
9
2
．
如图，矩形ABCD中，DC=
3
，AD=1，在DC上截取DE=1，将△ADE沿AE翻折到D'点，当D'在平面ABC上的射影落在AE上时，四棱锥D'-ABCE的体积是
2
6
-
2
12
2
6
-
2
12
；当D'在平面ABC上的射影落在AC上时，二面角D'-AE-B的平面角的余弦值是
2-
3
2-
3
．
（理）如图，矩形ABCD中，AB=1，BC=a，PA⊥平面ABCD
（1）问BC边上是否存在Q点，使
PQ
⊥
QD
，说明理由．
（2）问当Q点惟一，且cos＜
BP
，
QD
＞=
10
10
时，求点P的位置．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网