Question

【题目】已知椭圆的离心率为，椭圆的长轴长为4．

（1）求椭圆的方程；

（2）已知直线与椭圆交于两点，是否存在实数使得以线段为直径的圆恰好经过坐标原点？若存在，求出的值；若不存在，请说明理由．

Answer 1

【答案】（1）（2）存在，

【解析】

（1）利用椭圆的长轴长为4，可得，结合离心率可得，从而可得方程；

（2）联立方程，结合韦达定理，验证是否成立即可.

（1）设椭圆的半焦距为，则由题设，得：，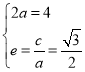

解得，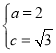

所以，

故所求椭圆的方程为.

（2）存在实数使得以线段为直径的圆恰好经过坐标原点．

理由如下：

设点，

将直线的方程代入，

并整理，得．（*）

则．

因为以线段为直径的圆恰好经过坐标原点，

所以，即．

又，

于是，

解得，

经检验知：此时（*）式的，符合题意．

所以当时，以线段为直径的圆恰好经过坐标原点．