题目内容
已知函数 (Ⅰ)设{an}是正数组成的数列,前n项和为Sn,其中a1=3.若点![]() (n∈N*)在函数y=f′(x)的图象上,求证:点(n,Sn)也在y=f′(x)的图象上;
(n∈N*)在函数y=f′(x)的图象上,求证:点(n,Sn)也在y=f′(x)的图象上;
(Ⅱ)求函数f(x)在区间(a-1,a)内的极值.
本小题主要考查函数极值、等差数列等基本知识,考查分类与整合、转化与化归等数学思想方法,考查分析问题和解决问题的能力.
(Ⅰ)证明:因为![]() 所以
所以![]() ,
,
由点![]() 在函数y=f′(x)的图象上,
在函数y=f′(x)的图象上,
得![]() =
=![]() ,即
,即![]() ,
,
又![]() 所以
所以![]() ,又因为a1=3,
,又因为a1=3,
所以数列{an}是以3为首项,公差为2的等差数列。
所以![]() ,又因为f′(x)=n2+2n,所以
,又因为f′(x)=n2+2n,所以![]() ,
,
故点![]() 也在函数y=f′(x)的图象上.
也在函数y=f′(x)的图象上.
(Ⅱ)解:![]() ,
,
由![]() 得
得![]() .当x变化时,
.当x变化时,![]() ﹑
﹑![]() 的变化情况如下表:
的变化情况如下表:
x | (-∞,-2) | -2 | (-2,0) | 0 | (0,+∞) |
f′(x) | + | 0 | - | 0 | + |
f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
注意到![]() ,从而
,从而
①当![]() ,此时
,此时![]() 无极小值;
无极小值;
②当![]() 的极小值为
的极小值为![]() ,此时
,此时![]() 无极大值;
无极大值;
③当![]() 既无极大值又无极小值.
既无极大值又无极小值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 :函数
:函数 的图像必过定点
的图像必过定点 ;命题
;命题 的图像关于
的图像关于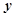 轴对称,则函数
轴对称,则函数 关于直线
关于直线 对称,那么
(
)
对称,那么
(
) 为真
B、
为真
B、 为假
为假 D、
D、