Question

已知关于x的方程2x²-(+1)x+m=0的两根为sinα和cosα，且α∈(0,2π).?

（1）求的值；

（2）求m的值；

（3）求方程的两根，及此时的角α.

Answer 1

思路分析：利用同角基本关系式和一元二次方程根与系数的关系解题.

解：（1）由一元二次方程根与系数的关系可得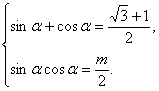

∴= =sinα+cosα=.

（2）由已知得sinα+cosα=，

∴(sinα+cosα)²=()²=1+2sinαcosα.

∴sinαcosα=，即=.

∴m=.

（3）当m=时，方程化为2x²-(3+1)x+=0，解得x₁=或x₂=.

∴或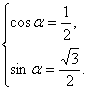

又∵α∈(0,2π)，∴α=或.

方法归纳 由三角函数的定义,可知一个三角函数值可以对应无数多个角，当已知三角函数值求角时，应注意角的范围，利用三角函数值和角的范围确定角的大小.