题目内容
四棱锥P—ABCD中,PA⊥底面ABCD,且![]() ,
,![]() ,
,![]() .
.
(1) 在侧棱PC上是否存在一点Q,使BQ//平面PAD?证明你的结论;
(2) 求证:平面PBC⊥平面PC D.
 |
(1) 解:当Q为侧棱PC中点时,有BQ//平面PA D.
证明如下:如图,取PD的中点E,连AE、EQ.
∵Q为PC中点,则EQ为△PCD的中位线,
∴EQ//CD且![]() .
.
∵AB//CD且![]() ,∴EQ//AB且EQ=AB,
,∴EQ//AB且EQ=AB,
∴四边形ABQE为平行四边形,则BQ//AE.
∵![]() 平面PAD,
平面PAD,![]() 平面PAD平面PAD,
平面PAD平面PAD,
∴![]() 平面PAD.
平面PAD.
(2) 证:∵PA⊥底面ABCD,∴ PA⊥CD.
∵AD⊥CD,![]() ,∴CD⊥平面PAD.
,∴CD⊥平面PAD.
∵![]() 平面PAD,∴ CD⊥AE.
平面PAD,∴ CD⊥AE.
∵PA=AD,E为PD中点,∴AE⊥PD.
∵![]() ,∴AE⊥平面PCD.
,∴AE⊥平面PCD.
∵BQ//AE,∴BQ⊥平面PCD.
∵![]() 平面PBC,∴平面PBC⊥平面PCD.
平面PBC,∴平面PBC⊥平面PCD.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
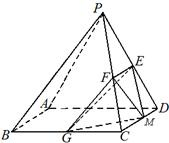 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.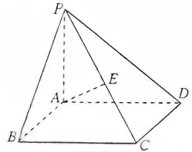 (2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
(2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC= 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.