题目内容
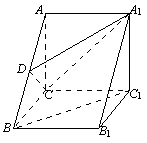
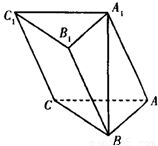
如图,在三棱柱![]() 中,
中,![]()
![]()
![]() 为
为![]() 的中点,且
的中点,且![]() .
.
(1) 求证:![]() ∥平面
∥平面![]() ;
;
(2) 求![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
 |
【命题意图】本小题主要考查立体几何的相关知识及空间想象能力,具体涉及到线面的平行关系、线面角的求法.
【试题解析】⑴证明:如图一,连结![]() 与
与![]() 交于点
交于点![]() ,连结
,连结![]() .
.
在△![]() 中,
中,![]() 、
、![]() 为中点,∴
为中点,∴![]() ∥
∥![]() . (4分)
. (4分)
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ∥平面
∥平面![]() . (6分)
. (6分)
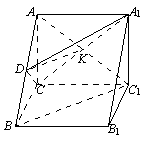
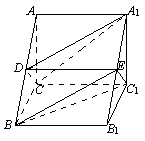
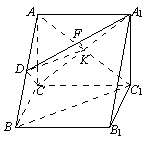
图一 图二 图三
⑵证明:(方法一)如图二,∵![]() 为
为![]() 的中点,∴
的中点,∴![]() .
.
又![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() . (8分)
. (8分)
取![]() 的中点
的中点![]() ,又
,又![]() 为
为![]() 的中点,∴
的中点,∴![]() 、
、![]() 、
、![]() 平行且相等,
平行且相等,
∴![]() 是平行四边形,∴
是平行四边形,∴![]() 、
、![]() 平行且相等.
平行且相等.
又![]() 平面
平面![]() ,∴
,∴![]()
![]() 平面
平面![]() ,∴∠
,∴∠![]() 即所求角. (10分)
即所求角. (10分)
由前面证明知![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ,∴此三棱柱为直棱柱.
,∴此三棱柱为直棱柱.
设![]() ∴
∴![]() ,
,![]() ,∠
,∠![]() =
=![]() . (12分)
. (12分)
(方法二)如图三,∵![]() 为
为![]() 的中点,∴
的中点,∴![]() .
.
又![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() . (8分)
. (8分)
取![]() 的中点
的中点![]() ,则
,则![]() ∥
∥![]() ,∴
,∴![]() 平面
平面![]() .
.
∴∠![]() 即
即![]() 与平面
与平面![]() 所成的角. (10分)
所成的角. (10分)
由前面证明知![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ,∴此三棱柱为直棱柱.
,∴此三棱柱为直棱柱.
设![]() ∴
∴![]() ,
,![]() ,∴∠
,∴∠![]() . (12分)
. (12分)

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 如图,在三棱柱中,已知AB⊥侧面BB1C1C,
如图,在三棱柱中,已知AB⊥侧面BB1C1C,

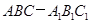 中,
中,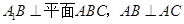 .
.
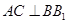 ;
;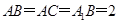 ,在棱
,在棱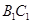 上确定一点P, 使二面角
上确定一点P, 使二面角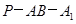 的平面角的余弦值为
的平面角的余弦值为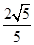 .
. 中,
中, ,顶点
,顶点 在底面
在底面 上的射影恰为点
上的射影恰为点 ,且
,且 .
. 平面
平面 ;
;
 与
与 所成的角的大小;
所成的角的大小; 为
为 的中点,并求出二面角
的中点,并求出二面角 的平面角的余弦值.
的平面角的余弦值.