题目内容

2．已知函数f（x）的图象是由函数h（x）=x2的图象向上平移1个单位长度得到的．（1）求f（x）的解析式：（2）设g（x）=f（x）-mx2，且在（0，2）上g′（x）＜0恒成立，求m的取值范围．

分析 （1）利用图象平移变换，可得f（x）的解析式；
（2）求导数，分离参数，即可得出结论．

解答 解：（1）∵函数f（x）的图象是由函数h（x）=x2的图象向上平移1个单位长度得到，
∴f（x）=x2+1；
（2）g（x）=f（x）-mx2=（1-m）x2+1，
∴g′（x）=2（1-m）x＜0在（0，2）上恒成立，
∴2（1-m）＜0
∴m＞1．

点评 本题考查函数的解析式，考查导数知识的运用，考查学生分析解决问题的能力，属于中档题．

练习册系列答案
相关题目
12．已知二次方程（2m+1）x2-2mx+（m-1）=0有且只有一个实根属于（1，2），且x=1，x=2都不是方程的根，求m的取值范围．
13．已知实数x，y满足ln（2x+2y）=0，则x+y的取值范围是（-∞，-2]．
10．已知过抛物线y2=2px（p＞0）的焦点F作一条直线交抛物线于A、B两点，以线段AB为直径的圆与直线x=-1相切，求该抛物线的方程．
17．解下列各一元二次不等式：
（1）（x+3）（x-1）＞-3；
（2）2x2-7x≤x2+12．
7．已知点A（cos77°，sin77°），B（cos17°，sin17°），则直线AB的斜率为（　　）
A．tan47°B．tan43°C．-tan47°D．-tan43°
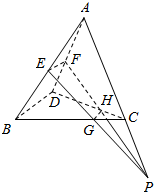14．已知空间四边形ABCD中，E，F分别是AB，AD的中点，G，H分别是BC，CD上的点，且$\frac{BG}{GC}=\frac{DH}{HC}$=2，求证：直线EG，FH，AC相交于同一点P．
11．等差数列{an}的前n项和为Sn，已知a1=10，a2为整数，且Sn≤S4．则通项公式an=13-3n．
16．定义在D上的函数f（x），如果满足：对任意x∈D，存在常数M＞0，都有|f（x）|≤M成立，则称f（x）是D上的有界函数，其中M称为函数f（x）的上界．已知函数$f（x）={（\frac{1}{4}）^x}+a•{（\frac{1}{2}）^x}-1$，g（x）=$\frac{1-m•{2}^{x}}{1+m•{2}^{x}}$．
（Ⅰ）当a=1时，求函数f（x）在（-∞，0）上的值域，并判断函数f（x）在（-∞，0）上是否为有界函数，请说明理由；
（Ⅱ）当m=1时，判断函数g（x）的奇偶性并证明，并判断g（x）是否有上界，并说明理由；
（Ⅱ）若函数f（x）在[0，+∞）上是以2为上界的有界函数，求实数a的取值范围；
（ IV）若m＞0，函数g（x）在[0，1]上的上界是G，求G的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网