题目内容
已知数列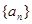 的各项均为正数,
的各项均为正数,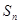 是数列
是数列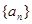 的前n项和,且
的前n项和,且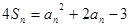 .
.
(1)求数列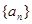 的通项公式;
的通项公式;
(2)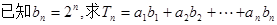 的值.
的值.
(1)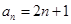 .(2)
.(2)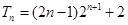 。
。
解析试题分析:(1)令n = 1,解出a1 =" 3," (a1 = 0舍),
由4Sn = an2 + 2an-3 ①
及当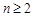 时 4sn-1 =
时 4sn-1 = 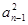 + 2an-1-3 ②
+ 2an-1-3 ②
①-②得到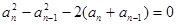 ,
,
确定得到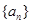 是以3为首项,2为公差的等差数列.
是以3为首项,2为公差的等差数列.
(2)利用“错位相减法”求和.
试题解析: (1)当n = 1时, 解出a1 =" 3," (a1 = 0舍) 1分
解出a1 =" 3," (a1 = 0舍) 1分
又4Sn = an2 + 2an-3 ①
当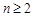 时 4sn-1 =
时 4sn-1 = 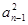 + 2an-1-3 ②
+ 2an-1-3 ②
①-②  , 即
, 即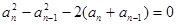 ,
,
∴  , 4分
, 4分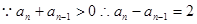 (
(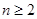 ),
),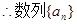 是以3为首项,2为公差的等差数列,
是以3为首项,2为公差的等差数列, 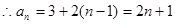 . 6分
. 6分
(2) ③
③
又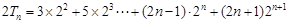 ④
④
④-③ 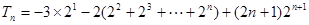
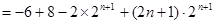
 12分
12分
考点:等差数列及其求和,等比数列的求和,“错位相减法”.

练习册系列答案
相关题目
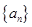 中,
中, ,则
,则 的前n项和是 .
的前n项和是 .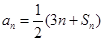 对一切正整数n成立
对一切正整数n成立 ,求数列
,求数列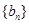 的前n项和
的前n项和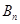 .
.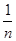 )+f(
)+f(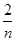 )+f(
)+f(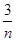 )+…+f(
)+…+f(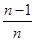 )+f(1).
)+f(1).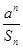 (a∈R)且bn<bn+1对所有正整数n恒成立,求a的取值范围.
(a∈R)且bn<bn+1对所有正整数n恒成立,求a的取值范围.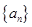 的前
的前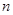 项和为
项和为 ,且
,且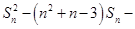
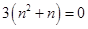 ,
, .
.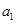 的值;
的值;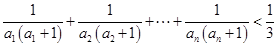 .
.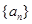 的前
的前 项和为
项和为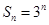 ,数列
,数列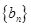 满足
满足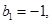
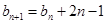 (
(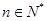 ).
).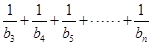 的值.
的值.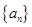 中,
中,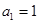 ,前
,前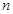 项的和是
项的和是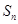 ,且
,且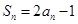 ,
,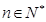 .
.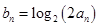 ,求
,求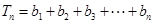 .
.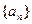 满足:
满足: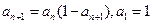 ,数列
,数列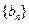 满足:
满足: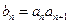 ,则数列
,则数列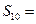 ;
;