题目内容
已知函数地f(x)的定义域是{x|x∈R,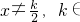 Z},且f(x)+f(2-x)=0,
Z},且f(x)+f(2-x)=0,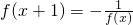 ,当
,当 时,f(x)=3x.
时,f(x)=3x.
(1)求证:f(x)是奇函数;
(2)求f(x)在区间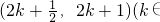 Z)上的解析式.
Z)上的解析式.
解:(1)由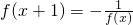 ,
,
得 ,
,
所以f(x)是周期为2的函数.
∴f(x)+f(2-x)=0,
即为f(x)+f(-x)=0,
故f(x)是奇函数.
(2)当x∈(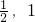 )时,
)时,
由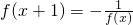 ,
,
知f(x)=f[1+(x-1)]
=-
=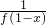
= .
.
所以,当x∈(2k+ ,2k+1),k∈Z)时,
,2k+1),k∈Z)时,
f(x)=f(x-2k)
= .
.
分析:(1)由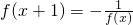 能导出f(x)是周期为2的函数.由此能够证明f(x)是奇函数.
能导出f(x)是周期为2的函数.由此能够证明f(x)是奇函数.
(2)当x∈(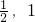 )时,f(x)=f[1+(x-1)]=-
)时,f(x)=f[1+(x-1)]=- =
=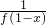 =
= .由此能够求出f(x)在区间
.由此能够求出f(x)在区间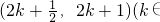 Z)上的解析式.
Z)上的解析式.
点评:本题证明函数是奇函数,求函数的解析式,解题时要认真审题,注意函数的周期性、奇偶性的灵活运用.
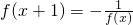 ,
,得
 ,
,所以f(x)是周期为2的函数.
∴f(x)+f(2-x)=0,
即为f(x)+f(-x)=0,
故f(x)是奇函数.
(2)当x∈(
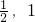 )时,
)时,由
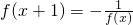 ,
,知f(x)=f[1+(x-1)]
=-

=
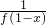
=
 .
.所以,当x∈(2k+
 ,2k+1),k∈Z)时,
,2k+1),k∈Z)时,f(x)=f(x-2k)
=
 .
.分析:(1)由
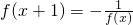 能导出f(x)是周期为2的函数.由此能够证明f(x)是奇函数.
能导出f(x)是周期为2的函数.由此能够证明f(x)是奇函数.(2)当x∈(
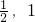 )时,f(x)=f[1+(x-1)]=-
)时,f(x)=f[1+(x-1)]=- =
=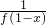 =
= .由此能够求出f(x)在区间
.由此能够求出f(x)在区间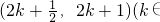 Z)上的解析式.
Z)上的解析式.点评:本题证明函数是奇函数,求函数的解析式,解题时要认真审题,注意函数的周期性、奇偶性的灵活运用.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
已知函数地f(x)=3x+cos2x+sin2x且a=f′(
),f′(x)是f(x)的导函数,则过曲线y=x3上一点P(a,b)的切线方程为( )
| π |
| 4 |
| A、3x-y-2=0 |
| B、4x-3y+1=0 |
| C、3x-y-2=0或3x-4y+1=0 |
| D、3x-y-2=0或4x-3y+1=0 |
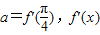 是f(x)的导函数,则过曲线y=x3上一点P(a,b)的切线方程为( )
是f(x)的导函数,则过曲线y=x3上一点P(a,b)的切线方程为( )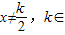 Z},且f(x)+f(2-x)=0,
Z},且f(x)+f(2-x)=0,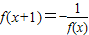 ,当
,当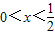 时,f(x)=3x.
时,f(x)=3x.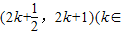 Z)上的解析式.
Z)上的解析式.