题目内容
.(本小题满分13分)
数列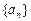 的前n项和
的前n项和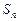 满足
满足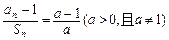 .数列
.数列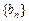 满足
满足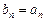 ·
·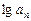 .
.
(1)求数列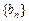 的前n项和
的前n项和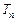 ;
;
(2)若对一切n∈N*都有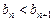 ,求a的取值范围.
,求a的取值范围.
数列
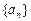 的前n项和
的前n项和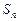 满足
满足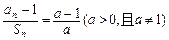 .数列
.数列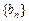 满足
满足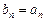 ·
·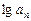 .
.(1)求数列
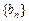 的前n项和
的前n项和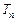 ;
;(2)若对一切n∈N*都有
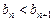 ,求a的取值范围.
,求a的取值范围.解:(1)当n=1时,a1=S1,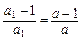 ,解得a1=a.………………1分
,解得a1=a.………………1分
当n≥2时,an="Sn-" Sn-1.
∵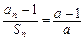 ,∴
,∴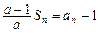 ,………………………2分
,………………………2分
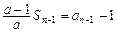 ,两式相减得
,两式相减得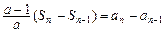 ,
,
∴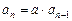 ,
,
所以数列{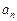 }是首项为a,公比为a的等比数列.
}是首项为a,公比为a的等比数列.
∴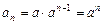 .…………………………………………3分
.…………………………………………3分
从而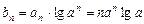 ,
,
∴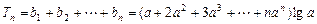 .
.
设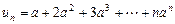 ,则
,则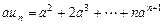 ,
,
∴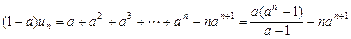 ,
,
∴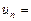
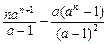 .
.
∴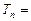
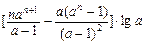 .………………………………6分
.………………………………6分
(2)由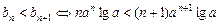 可得
可得
①当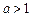 时,由
时,由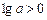 ,可得
,可得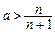 ,
,
∵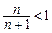 (n∈N*),
(n∈N*),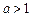 ,………………………………8分
,………………………………8分
∴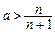 对一切n∈N*都成立,此时的解为
对一切n∈N*都成立,此时的解为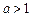 .
.
②当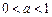 时,由
时,由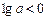 可得
可得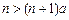 ,
,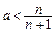
∵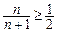 (n∈N*),
(n∈N*),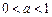 ,…………………………11分
,…………………………11分
 ∴
∴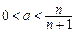 对一切n∈N*都成立,∴
对一切n∈N*都成立,∴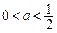 .
.
由①,②可知,对一切n∈N*都有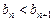 的a的取值范围是
的a的取值范围是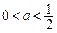 或
或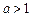 .13分
.13分
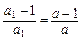 ,解得a1=a.………………1分
,解得a1=a.………………1分当n≥2时,an="Sn-" Sn-1.
∵
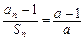 ,∴
,∴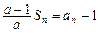 ,………………………2分
,………………………2分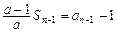 ,两式相减得
,两式相减得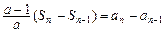 ,
,∴
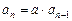 ,
,所以数列{
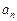 }是首项为a,公比为a的等比数列.
}是首项为a,公比为a的等比数列.∴
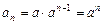 .…………………………………………3分
.…………………………………………3分从而
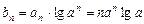 ,
,∴
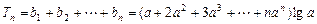 .
.设
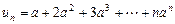 ,则
,则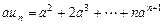 ,
,∴
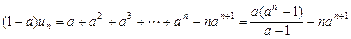 ,
,∴
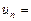
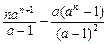 .
.∴
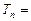
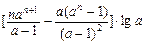 .………………………………6分
.………………………………6分(2)由
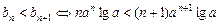 可得
可得①当
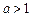 时,由
时,由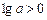 ,可得
,可得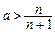 ,
,∵
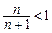 (n∈N*),
(n∈N*),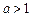 ,………………………………8分
,………………………………8分∴
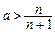 对一切n∈N*都成立,此时的解为
对一切n∈N*都成立,此时的解为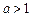 .
.②当
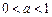 时,由
时,由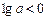 可得
可得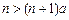 ,
,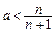
∵
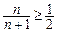 (n∈N*),
(n∈N*),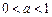 ,…………………………11分
,…………………………11分 ∴
∴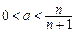 对一切n∈N*都成立,∴
对一切n∈N*都成立,∴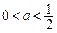 .
.由①,②可知,对一切n∈N*都有
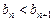 的a的取值范围是
的a的取值范围是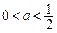 或
或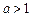 .13分
.13分略

练习册系列答案
相关题目
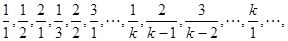 在这列数中,第
在这列数中,第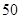 个值等于
个值等于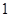 的项的序号是:
的项的序号是: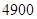
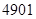
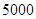
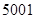
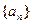 的前项和为
的前项和为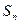 ,
,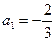 ,
,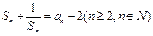
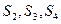
 达式,并用数学归纳法证明。
达式,并用数学归纳法证明。 为等差数列,
为等差数列,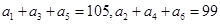 ,则
,则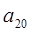 等于( )
等于( ) 数列
数列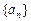 首项
首项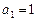 ,公差
,公差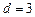 ,当
,当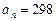 时,序号
时,序号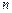 等于( )
等于( )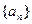 为等差数列,
为等差数列,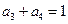 ,则其前
,则其前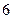 项之和为_____.
项之和为_____.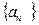 满足:
满足: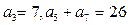 .
.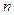 项和为
项和为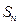
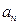 及
及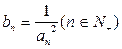 ,求数列
,求数列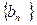 的前
的前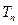 .
.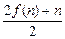 (n∈N*)且f(1)=2,则f(20)为( )
(n∈N*)且f(1)=2,则f(20)为( )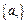 满足
满足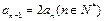 ,则
,则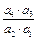 的值等于
的值等于