题目内容
 如下图,椭圆中心为O,F是焦点,A为顶点,准线l交OA延长线于B,P,Q在椭圆上且PD⊥l于D,QF⊥OA于F,则以下比值①
如下图,椭圆中心为O,F是焦点,A为顶点,准线l交OA延长线于B,P,Q在椭圆上且PD⊥l于D,QF⊥OA于F,则以下比值①| |PF| |
| |PD| |
| |QF| |
| |BF| |
| |AO| |
| |BO| |
| |AF| |
| |BA| |
| |FO| |
| |AO| |
①②③④⑤
①②③④⑤
(填写所有正确的序号)分析:根据题意,设椭圆的方程为
+
=1进而由椭圆的方程,分别化简表示、计算5个式子的值,与离心率e=
比较可得答案.
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| a |
解答:解:设椭圆的方程为
+
=1,(a>b>0)依次分析5个比值的式子可得:
①、根据椭圆的第二定义,可得 e=
故符合;
②、根据椭圆的性质,可得|BF|=
-c=
,|QF|=
,则
=
=e,故符合;
③、由椭圆的性质,可得|AO|=a,|BO|=
,则
=
=e,故符合;
④由椭圆的性质,可得
=e,故符合;
⑤、由椭圆的性质,可得|AO|=a,|FO|=c,
=
=e,故符合;
故答案为①②③④⑤
| x2 |
| a2 |
| y2 |
| b2 |
①、根据椭圆的第二定义,可得 e=
| |PF| |
| |PD| |
②、根据椭圆的性质,可得|BF|=
| a2 |
| c |
| b2 |
| c |
| b2 |
| a |
| |QF| |
| |BF| |
| c |
| a |
③、由椭圆的性质,可得|AO|=a,|BO|=
| a2 |
| c |
| |AO| |
| |BO| |
| c |
| a |
④由椭圆的性质,可得
| |AF| |
| |BA| |
⑤、由椭圆的性质,可得|AO|=a,|FO|=c,
| |FO| |
| |AO| |
| c |
| a |
故答案为①②③④⑤
点评:本题主要考查椭圆的性质,需要掌握椭圆的常见性质以及其中的一些特殊的长度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(本小题满分12分)
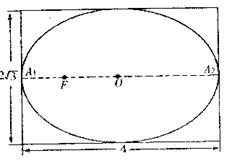
有一幅椭圆型彗星轨道图,长4cm,高![]() ,如下图,
,如下图,
已知O为椭圆中心,A1,A2是长轴两端点,
|
(Ⅰ)建立适当的坐标系,写出椭圆方程,
并求出当彗星运行到太阳正上方时二者在图上的距离;
(Ⅱ)直线l垂直于A1A2的延长线于D点,|OD|=4,
设P是l上异于D点的任意一点,直线A1P,A2P分别
交椭圆于M、N(不同于A1,A2)两点,问点A2能否
在以MN为直径的圆上?试说明理由.

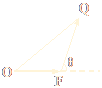
 ②
② ③
③ ④
④ ⑤
⑤ 能作为椭圆的离心率的是 (填写所有正确的序号)
能作为椭圆的离心率的是 (填写所有正确的序号)