题目内容
函数f(x)的导函数为f/(x),若(x+1)•f′(x)>0,则下列结论中正确的一项为
- A.x=-1一定是函数f(x)的极大值点
- B.x=-1一定是函数f(x)的极小值点
- C.x=-1不是函数f(x)的极值点
- D.x=-1不一定是函数f(x)的极值点
D
分析:由(x+1)•f/(x)>0,根据积商符号法则,分x>-1,x<-1,x=-1进行讨论,确定f′(x)>0或f′(x)<0,确定函数的单调性.
解答:∵(x+1)•f/(x)>0,
∴x>-1时,f′(x)>0,函数f(x)在区间(-1,+∞)单调递增,
x<-1时,f′(x)<0,函数f(x)在区间(-∞,-1)单调递减,
但是函数f(x)在x=-1处不一定可导,如f(x)=|x+1|= ,
,
x=-1不是函数f(x)的极值点.
故选D.
点评:考查x=x0是极值点是f′x0)=0的充分非必要条件,在判断x=-1两侧导数的符号,采取了分类讨论的数学思想,属基础题.
分析:由(x+1)•f/(x)>0,根据积商符号法则,分x>-1,x<-1,x=-1进行讨论,确定f′(x)>0或f′(x)<0,确定函数的单调性.
解答:∵(x+1)•f/(x)>0,
∴x>-1时,f′(x)>0,函数f(x)在区间(-1,+∞)单调递增,
x<-1时,f′(x)<0,函数f(x)在区间(-∞,-1)单调递减,
但是函数f(x)在x=-1处不一定可导,如f(x)=|x+1|=
 ,
,x=-1不是函数f(x)的极值点.
故选D.
点评:考查x=x0是极值点是f′x0)=0的充分非必要条件,在判断x=-1两侧导数的符号,采取了分类讨论的数学思想,属基础题.

练习册系列答案
相关题目
 已知函数f(x)的定义域为[-2,+∞),部分对应值如下表,
已知函数f(x)的定义域为[-2,+∞),部分对应值如下表,| x | -2 | 0 | 4 |
| f(x) | 1 | -1 | 1 |
| b+3 |
| a+3 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(-
|
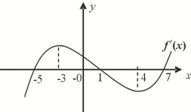 4、已知函数f(x)的导函数的图象如图所示,给出下列四个结论:
4、已知函数f(x)的导函数的图象如图所示,给出下列四个结论: