题目内容
已知等比数列{an}的通项公式为an=3n-1,设数列{bn}满足对任意自然数n都有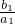 +
+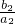 +
+ +┅+
+┅+ =2n+1恒成立.
=2n+1恒成立.
(1)求数列{bn}的通项公式; (2)求b1+b2+b3+┅+b2011的值.
解:(1)∵对任意正整数n,有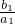 +
+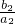 +
+ +┅+
+┅+ =2n+1,①
=2n+1,①
∴当n≥2时,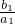 +
+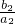 +
+ +┅+
+┅+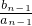 =2n-1,②…(4分)
=2n-1,②…(4分)
①-②得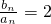 ; 故 bn=2an =2×3n-1(n≥2). …(7分)
; 故 bn=2an =2×3n-1(n≥2). …(7分)
当n=1时, ,
,
又a1=1,∴b1=3.
∴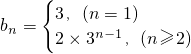 . …(10分)
. …(10分)
(2)b1+b2+b3+┅+b2011=3+(2×3+2×32+…+2×32010)=3+3(32010-1)=32011.…(15分)
分析:(1)把已知条件中的n换成n-1得到②,相减可得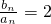 ,再由an=3n-1求出数列{bn}的通项公式.
,再由an=3n-1求出数列{bn}的通项公式.
(2)要求的式子即 3+(2×3+2×32+…+2×32010 ,利用等比数列的前n项和公式,求出要求式子的值.
点评:本题主要考查等比数列的通项公式,等比数列的前n项和公式,求得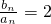 ,是解题的关键,属于中档题.
,是解题的关键,属于中档题.
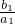 +
+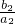 +
+ +┅+
+┅+ =2n+1,①
=2n+1,①∴当n≥2时,
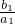 +
+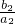 +
+ +┅+
+┅+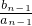 =2n-1,②…(4分)
=2n-1,②…(4分)①-②得
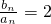 ; 故 bn=2an =2×3n-1(n≥2). …(7分)
; 故 bn=2an =2×3n-1(n≥2). …(7分)当n=1时,
 ,
,又a1=1,∴b1=3.
∴
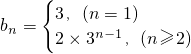 . …(10分)
. …(10分)(2)b1+b2+b3+┅+b2011=3+(2×3+2×32+…+2×32010)=3+3(32010-1)=32011.…(15分)
分析:(1)把已知条件中的n换成n-1得到②,相减可得
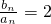 ,再由an=3n-1求出数列{bn}的通项公式.
,再由an=3n-1求出数列{bn}的通项公式.(2)要求的式子即 3+(2×3+2×32+…+2×32010 ,利用等比数列的前n项和公式,求出要求式子的值.
点评:本题主要考查等比数列的通项公式,等比数列的前n项和公式,求得
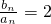 ,是解题的关键,属于中档题.
,是解题的关键,属于中档题. 
练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目