题目内容
若函数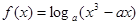
 在区间
在区间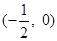 内单调递增,则
内单调递增,则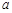 的取值范围是(▲)
的取值范围是(▲)
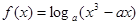
 在区间
在区间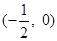 内单调递增,则
内单调递增,则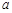 的取值范围是(▲)
的取值范围是(▲)A.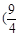 , ,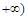 | B.(1, ) ) | C.[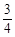 ,1) ,1) | D.[ ,1) ,1) |
C
本题考查简单复合函数的单调性,导数的应及分析问题解决问题的能力.
首先函数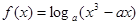
 在区间
在区间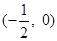 内有意义,则
内有意义,则
 设
设 ,则
,则 ,
, .
.
(1)当 时,
时, 是增函数,要使函数
是增函数,要使函数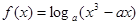
 在区间
在区间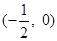 内单调递增,需使
内单调递增,需使 在区间
在区间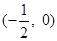 内内单调递增,则需使
内内单调递增,则需使
 对任意
对任意 恒成立,即
恒成立,即 对任意
对任意 恒成立;因为
恒成立;因为 时,
时, ,所以
,所以 与
与 矛盾,此时不成立.
矛盾,此时不成立.
(2) 当 时,
时, 是减函数,要使函数
是减函数,要使函数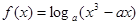
 在区间
在区间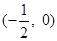 内单调递增,需使
内单调递增,需使 在区间
在区间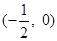 内内单调递减,则需使
内内单调递减,则需使
 对任意
对任意 恒成立,即
恒成立,即 对任意
对任意 恒成立;因为
恒成立;因为 时,
时, ,所以
,所以 满足
满足 此时
此时
综上: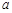 的取值范围是
的取值范围是 故选C
故选C
首先函数
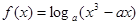
 在区间
在区间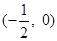 内有意义,则
内有意义,则 设
设 ,则
,则 ,
, .
.(1)当
 时,
时, 是增函数,要使函数
是增函数,要使函数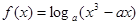
 在区间
在区间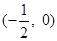 内单调递增,需使
内单调递增,需使 在区间
在区间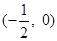 内内单调递增,则需使
内内单调递增,则需使 对任意
对任意 恒成立,即
恒成立,即 对任意
对任意 恒成立;因为
恒成立;因为 时,
时, ,所以
,所以 与
与 矛盾,此时不成立.
矛盾,此时不成立.(2) 当
 时,
时, 是减函数,要使函数
是减函数,要使函数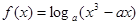
 在区间
在区间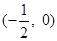 内单调递增,需使
内单调递增,需使 在区间
在区间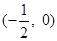 内内单调递减,则需使
内内单调递减,则需使 对任意
对任意 恒成立,即
恒成立,即 对任意
对任意 恒成立;因为
恒成立;因为 时,
时, ,所以
,所以 满足
满足 此时
此时
综上:
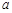 的取值范围是
的取值范围是 故选C
故选C
练习册系列答案
相关题目
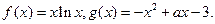
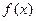 在
在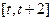
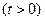 上的最小值;
上的最小值;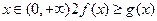 恒成立,求实数
恒成立,求实数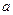 的取值范围;
的取值范围;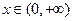 ,都有
,都有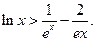
 ,
, ,
, ,则a,b,c三个数的大小关系是
,则a,b,c三个数的大小关系是



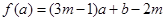 ,当
,当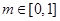 时,
时,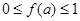 恒成立,则
恒成立,则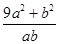

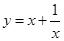 在
在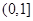 上是减函数,在
上是减函数,在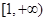 上是增函数;函数
上是增函数;函数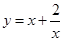 在
在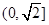 上是减函数,在
上是减函数,在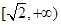 上是增函数;函数
上是增函数;函数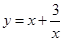 在
在 上是减函数,在
上是减函数,在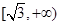 上是增函数;……利用上述所提供的信息解决问题:若函数
上是增函数;……利用上述所提供的信息解决问题:若函数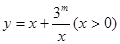 的值域是
的值域是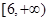 ,则实数
,则实数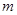 的值是
的值是 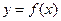 是定义在
是定义在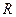 上的增函数,函数
上的增函数,函数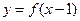 的图象关于点
的图象关于点 (1 , 0)对称,若对任意的
(1 , 0)对称,若对任意的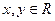 ,不等式
,不等式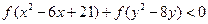 恒成立,则当
恒成立,则当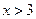 时,
时,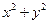 的取值范围是____▲_____
的取值范围是____▲_____ ,有下列命题:
,有下列命题: 轴对称;
轴对称; 时,
时, 是增函数;当
是增函数;当 时,
时, ;
; 在区间(-1,0)、(2,+∞)上是增函数;
在区间(-1,0)、(2,+∞)上是增函数;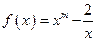 ,且
,且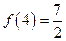 。
。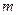 的值;
的值;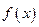 的奇偶性;
的奇偶性;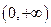 上的单调性,并给予证明。
上的单调性,并给予证明。 的值域为 。
的值域为 。