题目内容
一个几何体的三视图如图所示分别是直角梯形、正方形和矩形,画出直观图,并求它的体积与表面积.
分析:由三视图可以知道,此几何体是一个直四棱柱,其体积可以用梯形的面积乘以高来求,四个侧面都是矩形,其底面是一个直角梯形,故可以根据三视图求出相应的边长,利用面积公式与体积公式求值即可.
解答:解:几何体是一个以直角梯形为底面的直四棱柱.
由三视图得:此棱柱的高是1,底面直角梯形的两个底边长分别为1与2,垂直于底边的腰长度是1,故与底边不垂直的腰的长度为
∴V=S梯形×1=
(1+2)×1×1=
S表=2×
×(1+2)×1+1×(1+2+1+
)=3+4+
=7+
故此梯形的体积是
,其表面积是7+
由三视图得:此棱柱的高是1,底面直角梯形的两个底边长分别为1与2,垂直于底边的腰长度是1,故与底边不垂直的腰的长度为
| 2 |
∴V=S梯形×1=
| 1 |
| 2 |
| 3 |
| 2 |
S表=2×
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
故此梯形的体积是
| 3 |
| 2 |
| 2 |
点评:本题考点是由三视图求面积与体积,本题主要考查根据三视图的作图规则还原实物图的能力,三视图的作图规则是主视图与俯视图长对正,主视图与侧视图高平齐,侧视图与俯视图是宽相等,本题是考查利用三视图的作图规则把三视图中的数据还原到原始图形中来,求面积与体积,做题时要注意正确利用三视图中所提供的信息,正确地得出实物图的长宽高等数据.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
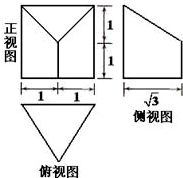
 (2013•房山区二模)一个几何体的三视图如图所示,则这个几何体的表面积为( )
(2013•房山区二模)一个几何体的三视图如图所示,则这个几何体的表面积为( )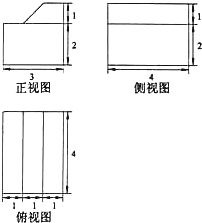 (2012•天津)一个几何体的三视图如图所示(单位:m),则该几何体的体积为
(2012•天津)一个几何体的三视图如图所示(单位:m),则该几何体的体积为 一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的表面积为
一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的表面积为 (2010•河东区一模)一个几何体的三视图如图所示,则该几何体(不考虑接触点)的表面积为
(2010•河东区一模)一个几何体的三视图如图所示,则该几何体(不考虑接触点)的表面积为