题目内容
已知椭圆C的中心在坐标原点O,焦点在x轴上,离心率为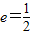 ,P为椭圆上一动点.F1、F2分别为椭圆的左、右焦点,且△PF1F2面积的最大值为
,P为椭圆上一动点.F1、F2分别为椭圆的左、右焦点,且△PF1F2面积的最大值为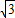 .
.(I)求椭圆C的方程;
(II)设直线l与圆x2+y2=1相切且与椭圆C相交于A、B两点,求
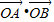 的取值范围.
的取值范围.
【答案】分析:(I)设出椭圆的方程,利用离心率和a,b与c的关系求得a和b的关系,根据椭圆的几何性质知,当点P为椭圆的短轴端点时,△PF1F2的面积最大,进而求得bc的关系,最后联立求得a和b,则椭圆的方程可得.
(II)先对直线l的斜率分类讨论,当直线l的斜率不存在时,求出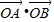 的值;当直线l的斜率存在时,设l:y=kx+m,联立l与椭圆C的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量的数量积坐标公式即可求得
的值;当直线l的斜率存在时,设l:y=kx+m,联立l与椭圆C的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量的数量积坐标公式即可求得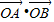 的取值范围,从而解决问题.
的取值范围,从而解决问题.
解答:解:(I)设椭圆C1的方程为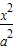 +
+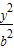 =1(a>b>0),c=
=1(a>b>0),c=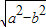 ,
,
则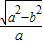 =
= ,所以
,所以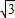 a=2b、
a=2b、
由椭圆的几何性质知,当点P为椭圆的短轴端点时,
△PF1F2的面积最大,故|F1F2|b=bc=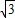 ,
,
解得a=2,b=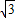 .
.
故所求椭圆方程为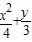 =1.
=1.
(II)当直线l的斜率不存在时,因l与与圆x2+y2=1相切,∴l:x=1,此时A(1, ),
),
B(1,- ),∴
),∴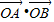 =1-
=1- =
= ;
;
当直线l的斜率存在时,设l:y=kx+m,因l与与圆x2+y2=1相切,∴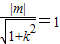 ,整理得m2=k2+1,
,整理得m2=k2+1,
联立l与椭圆C的方程,消去y得(4k2+3)x2+8kmx+4m2-12=0,
△=48(4k2+3-m2)=48(3k2+2)>0,设A(x1,y1),B(x2,y2),
则x1+x2=-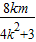 ,
,
x1x2=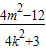 ,
,
∴y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=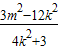
∴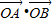 =x1x2+y1y2=
=x1x2+y1y2=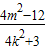 +
+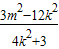 =
=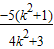 =-
=- -
-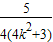
∵4k2+3≥3,
∴0<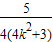
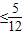 ,-
,- ≤
≤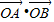 <-
<- .
.
综上,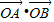 的取值范围是[-
的取值范围是[- ,-
,- ].
].
点评:本题考查的知识点是直线与圆的位置关系,直线与圆锥曲线的综合应用,其中根据已知条件求出椭圆的标准方程是解答本题的关键.
(II)先对直线l的斜率分类讨论,当直线l的斜率不存在时,求出
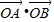 的值;当直线l的斜率存在时,设l:y=kx+m,联立l与椭圆C的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量的数量积坐标公式即可求得
的值;当直线l的斜率存在时,设l:y=kx+m,联立l与椭圆C的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量的数量积坐标公式即可求得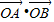 的取值范围,从而解决问题.
的取值范围,从而解决问题.解答:解:(I)设椭圆C1的方程为
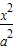 +
+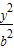 =1(a>b>0),c=
=1(a>b>0),c=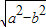 ,
,则
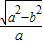 =
= ,所以
,所以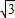 a=2b、
a=2b、由椭圆的几何性质知,当点P为椭圆的短轴端点时,
△PF1F2的面积最大,故|F1F2|b=bc=
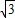 ,
,解得a=2,b=
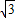 .
.故所求椭圆方程为
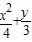 =1.
=1.(II)当直线l的斜率不存在时,因l与与圆x2+y2=1相切,∴l:x=1,此时A(1,
 ),
),B(1,-
 ),∴
),∴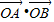 =1-
=1- =
= ;
;当直线l的斜率存在时,设l:y=kx+m,因l与与圆x2+y2=1相切,∴
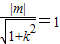 ,整理得m2=k2+1,
,整理得m2=k2+1,联立l与椭圆C的方程,消去y得(4k2+3)x2+8kmx+4m2-12=0,
△=48(4k2+3-m2)=48(3k2+2)>0,设A(x1,y1),B(x2,y2),
则x1+x2=-
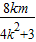 ,
,x1x2=
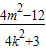 ,
,∴y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=
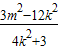
∴
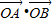 =x1x2+y1y2=
=x1x2+y1y2=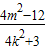 +
+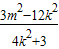 =
=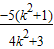 =-
=- -
-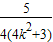
∵4k2+3≥3,
∴0<
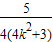
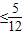 ,-
,- ≤
≤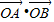 <-
<- .
.综上,
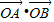 的取值范围是[-
的取值范围是[- ,-
,- ].
].点评:本题考查的知识点是直线与圆的位置关系,直线与圆锥曲线的综合应用,其中根据已知条件求出椭圆的标准方程是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知椭圆C的中心在坐标原点,焦点在x轴上,左、右焦点分别为F1,F2,且|F1F2|=2,点P(1,
已知椭圆C的中心在坐标原点,焦点在x轴上,左、右焦点分别为F1,F2,且|F1F2|=2,点P(1,