题目内容
18.设曲线(2x+y-4)(x-y-2)=0与抛物线y=-$\frac{1}{8}$x2的准线围成的三角形区域(包含边界)为m,则z=$\frac{y}{x+1}$的最大值是1.分析 作出出三角形区域,z的几何意义是区域内的点到定点D(-1,0)的斜率,利用数形结合进行求解即可.
解答 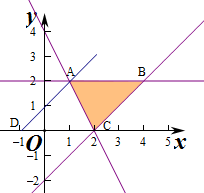 解:由(2x+y-4)(x-y-2)=0得2x+y-4=0或x-y-2=0,
解:由(2x+y-4)(x-y-2)=0得2x+y-4=0或x-y-2=0,
抛物线的标准方程为x2=-8y,准线方程为y=2,
作出对应的区域如图:
z=$\frac{y}{x+1}$的几何意义是区域内的点到定点D(-1,0)的斜率,
由图象知AD的斜率最大,
由$\left\{\begin{array}{l}{y=2}\\{2x+y-4=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,即A(1,2),
则z=$\frac{y}{x+1}$的最大值是z=$\frac{2}{1+1}$=1,
故答案为:1.
点评 本题主要考查线性规划的应用,利用条件作出对应区域,结合直线斜率公式是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.如图直观图由直三棱柱与圆锥组成的几何体,其三视图的正视图为正方形,则俯视图中的椭圆的离心率为( )


| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{2}$ |
13.在复平面内,复数$\frac{{i}^{2015}}{1+i}$对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.在△ABC中,$c=\sqrt{2}$,acosC=csinA,若当a=x0时的△ABC有两解,则x0的取值范围是( )
| A. | $(1,\sqrt{2})$ | B. | $(1,\sqrt{3})$ | C. | $(\sqrt{3},2)$ | D. | $(\sqrt{2},2)$ |