题目内容
若变量x,y满足约束条件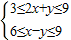 则z=x+2y的最小值为 .
则z=x+2y的最小值为 .
【答案】分析:在坐标系中画出约束条件的可行域,得到的图形是一个平行四边形,把目标函数z=x+2y变化为y=- x+
x+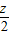 ,当直线沿着y轴向上移动时,z的值随着增大,当直线过A点时,z取到最小值,求出两条直线的交点坐标,代入目标函数得到最小值.
,当直线沿着y轴向上移动时,z的值随着增大,当直线过A点时,z取到最小值,求出两条直线的交点坐标,代入目标函数得到最小值.
解答: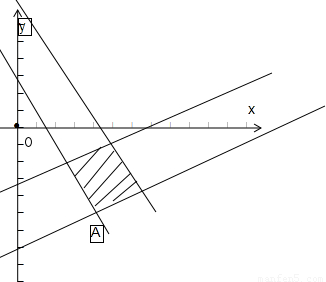 解:在坐标系中画出约束条件的可行域,
解:在坐标系中画出约束条件的可行域,
得到的图形是一个平行四边形,
目标函数z=x+2y,
变化为y=- x+
x+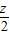 ,
,
当直线沿着y轴向上移动时,z的值随着增大,
当直线过A点时,z取到最小值,
由y=x-9与2x+y=3的交点得到A(4,-5)
∴z=4+2(-5)=-6
故答案为:-6
点评:本题考查线性规划问题,考查根据不等式组画出可行域,在可行域中,找出满足条件的点,把点的坐标代入,求出最值.
 x+
x+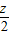 ,当直线沿着y轴向上移动时,z的值随着增大,当直线过A点时,z取到最小值,求出两条直线的交点坐标,代入目标函数得到最小值.
,当直线沿着y轴向上移动时,z的值随着增大,当直线过A点时,z取到最小值,求出两条直线的交点坐标,代入目标函数得到最小值.解答:
 解:在坐标系中画出约束条件的可行域,
解:在坐标系中画出约束条件的可行域,得到的图形是一个平行四边形,
目标函数z=x+2y,
变化为y=-
 x+
x+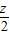 ,
,当直线沿着y轴向上移动时,z的值随着增大,
当直线过A点时,z取到最小值,
由y=x-9与2x+y=3的交点得到A(4,-5)
∴z=4+2(-5)=-6
故答案为:-6
点评:本题考查线性规划问题,考查根据不等式组画出可行域,在可行域中,找出满足条件的点,把点的坐标代入,求出最值.

练习册系列答案
相关题目