题目内容
对两个变量y和x进行回归分析,得到一组样本数据:(x1,y1),(x2,y2),…,(xn,yn),则下列说法中不正确的是( )A.由样本数据得到的回归方程
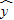 =
=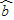 x+
x+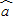 必过样本中心(
必过样本中心(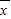 ,
,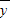 )
)B.残差平方和越小的模型,拟合的效果越好
C.用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好
D.直线
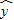 =
=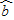 x+
x+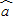 和各点(x1,y1),(x2,y2),…,(xn,yn)的偏差
和各点(x1,y1),(x2,y2),…,(xn,yn)的偏差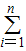 [yi-(
[yi-(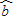 xi+
xi+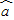 )]2是该坐标平面上所有直线与这些点的偏差中最小的
)]2是该坐标平面上所有直线与这些点的偏差中最小的
【答案】分析:线性回归方程一定过样本中心点,在一组模型中残差平方和越小,拟合效果越好,相关指数表示拟合效果的好坏,指数越小,相关性越强.
解答:解:样本中心点在直线上,故A正确,
残差平方和越小的模型,拟合效果越好,故B正确,
R2越大拟合效果越好,故C不正确,
直线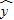 =
=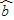 x+
x+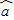 和各点(x1,y1),(x2,y2),…,(xn,yn)的偏差
和各点(x1,y1),(x2,y2),…,(xn,yn)的偏差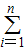 [yi-(
[yi-(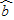 xi+
xi+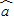 )]2是该坐标平面上所有直线与这些点的偏差中最小的,故D正确,
)]2是该坐标平面上所有直线与这些点的偏差中最小的,故D正确,
故选C
点评:本题考查衡量两个变量之间相关关系的方法,要想知道两个变量之间的有关或无关的精确的可信程度,只有利用独立性检验的有关计算,才能做出判断.
解答:解:样本中心点在直线上,故A正确,
残差平方和越小的模型,拟合效果越好,故B正确,
R2越大拟合效果越好,故C不正确,
直线
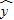 =
=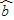 x+
x+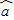 和各点(x1,y1),(x2,y2),…,(xn,yn)的偏差
和各点(x1,y1),(x2,y2),…,(xn,yn)的偏差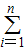 [yi-(
[yi-(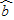 xi+
xi+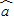 )]2是该坐标平面上所有直线与这些点的偏差中最小的,故D正确,
)]2是该坐标平面上所有直线与这些点的偏差中最小的,故D正确,故选C
点评:本题考查衡量两个变量之间相关关系的方法,要想知道两个变量之间的有关或无关的精确的可信程度,只有利用独立性检验的有关计算,才能做出判断.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
对两个变量y和x进行回归分析,得到一组样本数据:(x1,y1),(x2,y2),…,(xn,yn),则下列说法中不正确的是( )
A、由样本数据得到的回归方程
| ||||||||||
| B、残差平方和越小的模型,拟合的效果越好 | ||||||||||
| C、用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好 | ||||||||||
| D、若变量y和x之间的相关系数为r=-0.9362,则变量y和x之间具有线性相关关系 |
对两个变量y和x进行回归分析,得到一组样本数据:(x1,y1),(x2,y2),…,(xn,yn),则下列说法中不正确的是
( )
( )
A、由样本数据得到的回归方程
| ||||||||||
| B、用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好 | ||||||||||
| C、残差平方和越小的模型,拟合的效果越好 | ||||||||||
| D、在线性回归模型中,R2=0.92表示解释变量解释了92%的预报变量 |
