题目内容
随机变量X的分布列如下表，求常数a.X | -1 | 0 | 1 | 2 | 3 |
P | 0.16 |
| a2 |
| 0.3 |
解：由离散型随机变量X的概率分布列的性质（2）知：
0.16+
+a2+
+0.3=1,
∴10a2+3a-5.4=0.
∴a=
或a=-
.
又由分布列的性质（1）知：概率的数值不可能为负，
∴a=-
舍去.
故所求常数a=
.
绿色通道:离散型随机变量的概率分布列的性质指的是表中的第二行概率的特点，而且，离散型随机变量在某个范围内取值的概率等于它取这个范围内各个值的概率之和.
练习册系列答案
名校通行证有效作业系列答案
相关题目
已知离散型随机变量X的分布列如表．若EX=0，DX=1，则a= ，b= ．
| X | -1 | 0 | 1 | 2 | ||
| P | a | b | c |
|
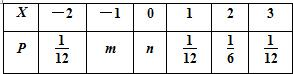已知随机变量X的分布列如图：其中m，n∈[0，1），且E（X）=| 1 |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知随机变量X的分布列如图，若EX=3，则b= ．
| X | B | 2 | 4 | ||||
| P | a |
|
|
已知离散型随机变量X 的分布列如右图．若E（X）=0，D（X）=1，则a、b、c的值依次为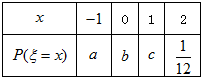
已知离散型随机变量x的分布列如右表．若Eξ=0，Dξ=1，则符合条件的一组数（a，b，c）=