题目内容
.(本题12分)已知函数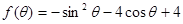 ,
,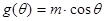
(1) 对任意的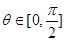 ,若
,若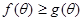 恒成立,求m取值范围;
恒成立,求m取值范围;
(2) 对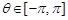 ,
,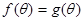 有两个不等实根,求m的取值范围.
有两个不等实根,求m的取值范围.
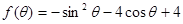 ,
,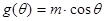
(1) 对任意的
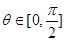 ,若
,若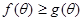 恒成立,求m取值范围;
恒成立,求m取值范围;(2) 对
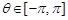 ,
,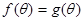 有两个不等实根,求m的取值范围.
有两个不等实根,求m的取值范围.(1)m
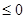 .(2)
.(2)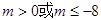 .
.(1)先把函数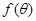 转化为
转化为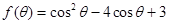 ,
,
(1)对任意的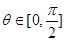 ,若
,若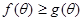 恒成立,转化为
恒成立,转化为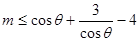 恒成立问题,然后构造函数求
恒成立问题,然后构造函数求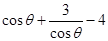 的最小值即可.
的最小值即可.
(2)解本小题的关键是把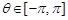 ,
,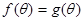 ,即
,即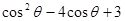
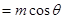 有两个不同的实根的问题,通过令
有两个不同的实根的问题,通过令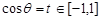 ,则命题转化为:
,则命题转化为: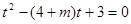 在
在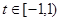 上有唯一的实根的常规问题来解决.
上有唯一的实根的常规问题来解决.
解: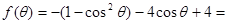
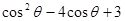
(1)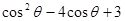
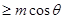 ,
,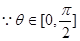
 ,
,
ⅰ:当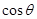 =0时,对任意m恒成立;
=0时,对任意m恒成立;
ⅱ:当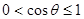 时,
时,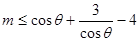 ,令
,令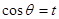 ,
,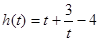 ,
,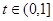 单调递减,当t=1时,
单调递减,当t=1时, ,所以m
,所以m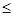
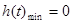 ;综上m
;综上m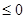 .……6分
.……6分
(3)(2)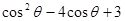
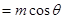 ,令
,令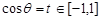 ,则命题转化为:
,则命题转化为: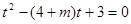 在
在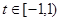 上有唯一的实根.ⅰ:
上有唯一的实根.ⅰ: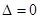 ,
,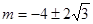 ,经检验当
,经检验当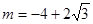 时,
时,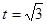 ,当
,当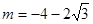 时,
时,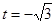 ,均不符合题意舍去;ⅱ:
,均不符合题意舍去;ⅱ: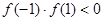 ,解得:m>0或m<-8;ⅲ
,解得:m>0或m<-8;ⅲ
(4)f(-1)=0,解得m=-8,此时有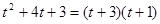 =0,符合题意;综上所述:
=0,符合题意;综上所述: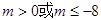 .
.
12分
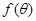 转化为
转化为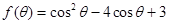 ,
,(1)对任意的
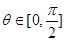 ,若
,若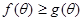 恒成立,转化为
恒成立,转化为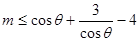 恒成立问题,然后构造函数求
恒成立问题,然后构造函数求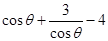 的最小值即可.
的最小值即可.(2)解本小题的关键是把
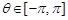 ,
,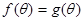 ,即
,即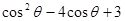
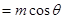 有两个不同的实根的问题,通过令
有两个不同的实根的问题,通过令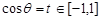 ,则命题转化为:
,则命题转化为: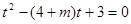 在
在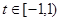 上有唯一的实根的常规问题来解决.
上有唯一的实根的常规问题来解决.解:
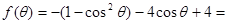
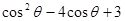
(1)
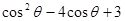
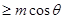 ,
,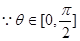
 ,
,ⅰ:当
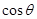 =0时,对任意m恒成立;
=0时,对任意m恒成立;ⅱ:当
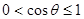 时,
时,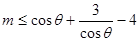 ,令
,令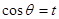 ,
,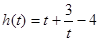 ,
,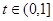 单调递减,当t=1时,
单调递减,当t=1时, ,所以m
,所以m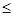
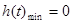 ;综上m
;综上m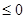 .……6分
.……6分(3)(2)
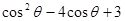
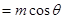 ,令
,令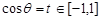 ,则命题转化为:
,则命题转化为: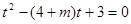 在
在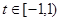 上有唯一的实根.ⅰ:
上有唯一的实根.ⅰ: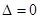 ,
,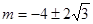 ,经检验当
,经检验当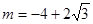 时,
时,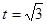 ,当
,当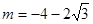 时,
时,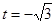 ,均不符合题意舍去;ⅱ:
,均不符合题意舍去;ⅱ: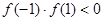 ,解得:m>0或m<-8;ⅲ
,解得:m>0或m<-8;ⅲ(4)f(-1)=0,解得m=-8,此时有
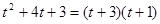 =0,符合题意;综上所述:
=0,符合题意;综上所述: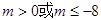 .
.12分

练习册系列答案
相关题目
 且
且 ,则角
,则角 是( )
是( )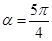 ,求
,求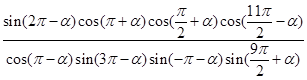 的值。
的值。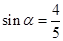 ,
,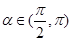 ,
,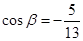 ,
,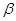 是第三象限角,求
是第三象限角,求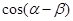 的值。
的值。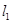 的方程为
的方程为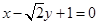 ,其倾斜角为
,其倾斜角为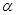 .过点
.过点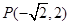 的直线
的直线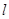 的倾斜角为
的倾斜角为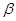 ,且
,且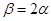 .
.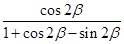 的值.
的值.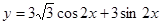 的最大值为_____________
的最大值为_____________ 为第三象限的角,
为第三象限的角, ,则
,则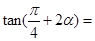 .
. =
= 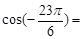 ( )
( )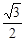
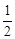
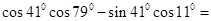 .
.