题目内容
用总长为14.8m的钢条制作一个长方体容器的框架,如果所制作容器的底面的一边比另一边长0.5m,那么高为多少时容器的容积最大?并求出它的最大容积.
当高为 时,容器的容积最大,最大容积为
时,容器的容积最大,最大容积为 .
.
解析试题分析:先设容器底面短边长为 ,利用长方体的体积公式求得其容积表达式,再利用导数研究它的单调性,进而得出此函数的最大值即可.
,利用长方体的体积公式求得其容积表达式,再利用导数研究它的单调性,进而得出此函数的最大值即可.
试题解析:设容器底面短边的边长为 ,容积为
,容积为 ,则底面另一边长为
,则底面另一边长为 ,高为:
,高为: .
.
由题意知: ,
, ,
,
则 .
.
令 ,解之得:
,解之得: (舍去).
(舍去).
又当 时,
时, 为增函数;当
为增函数;当 时,
时, 为减函数.
为减函数.
所以 在
在 时取得极大值
时取得极大值 ,这个极大值就是
,这个极大值就是 在
在 时的最大值,即
时的最大值,即 ,此时容器的高为1.2.
,此时容器的高为1.2.
所以当高为 时,容器的容积最大,最大值为
时,容器的容积最大,最大值为 .
.
考点:函数模型的选择与应用.

练习册系列答案
相关题目
为了研究玉米品种对产量的影响,某农科院对一块试验田种植的一批玉米共10000株的生长情况进行研究,现采用分层抽样方法抽取50株为样本,统计结果如下:
| | 高茎 | 矮茎 | 合计 |
| 圆粒 | 11 | 19 | 30 |
| 皱粒 | 13 | 7 | 20 |
| 合计 | 24 | 26 | 50 |
(2)根据对玉米生长情况作出的统计,是否能在犯错误的概率不超过0.050的前提下认为玉米的圆粒与玉米的高茎有关?(下面的临界值表和公式可供参考):
| P(K2≥k) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
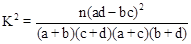 ,其中n=a+b+c+d为样本容量.
,其中n=a+b+c+d为样本容量.  ,函数
,函数 .
. 时,函数
时,函数 的图象与函数
的图象与函数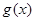 的图象有公共点,求实数
的图象有公共点,求实数 的最大值;
的最大值; 时,试判断函数
时,试判断函数 的上方?若能,求出
的上方?若能,求出 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.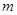 (单位:万元)的关系有经验公式
(单位:万元)的关系有经验公式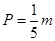 ,
, 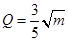 . 今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资
. 今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资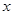 (单位:万元)
(单位:万元)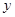 (单位:万元)关于
(单位:万元)关于 万件,则需另投入成本
万件,则需另投入成本 (万元)。已知A产品年产量不超过80万件时,
(万元)。已知A产品年产量不超过80万件时, ;A产品年产量大于80万件时,
;A产品年产量大于80万件时, 。因设备限制,A产品年产量不超过200万件。现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完。设该厂生产A产品的年利润为L(万元)。
。因设备限制,A产品年产量不超过200万件。现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完。设该厂生产A产品的年利润为L(万元)。 ;
;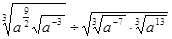 ;
;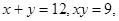 且
且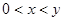 ,求
,求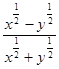 的值.
的值. (分贝)由公式
(分贝)由公式 (
( 为非零常数)给出,其中
为非零常数)给出,其中 为声音能量.
为声音能量. 满足
满足 时,求对应的声音能量
时,求对应的声音能量 满足的等量关系式;
满足的等量关系式; 时,声音强度为30分贝;当人们正常说话,声音能量为
时,声音强度为30分贝;当人们正常说话,声音能量为 时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪.
时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪.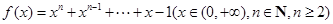 .
.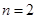 ,
,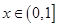 时,若不等式
时,若不等式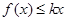 恒成立,求
恒成立,求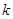 的范围;
的范围; 在
在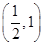 内存在零点.
内存在零点. 为奇函数.
为奇函数.  的最小正周期是
的最小正周期是 ;②函数
;②函数 ,0)
,0) 对称;④函数
对称;④函数
