题目内容
【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是直角梯形，AD⊥AB，AB∥DC，PA⊥底面ABCD，点E为棱PC的中点．AD=DC=AP=2AB=2．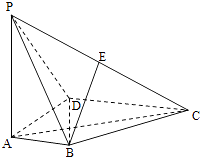 
（1）证明：BE⊥平面PDC；
（2）若F为棱PC上一点，满足BF⊥AC，求二面角F﹣AD﹣C的余弦值．
【答案】
（1）证明：∵PA⊥底面ABCD，AD⊥AB，
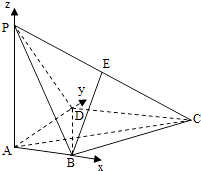
以A为坐标原点，建立如图所示的空间直角坐标系，
∵AD=DC=AP=2AB=2，∴AB=1，点E为棱PC的中点．
∴B（1，0，0），C（2，2，0），D（0，2，0），P（0，0，2），
E（1，1，1）
∴ 
=（0，1，1）， 
=（2，0，0）， 
=（0，2，﹣2）
∵ =0， =0，
∴BE⊥DC；BE⊥PD，
∵DC∩PD=D，
∴BE⊥平面PDC
（2）解：∵ 
=（1，2，0）， 
=（﹣2，﹣2，2）， 
=（2，2，0），
由F点在棱PC上，设 
=λ =（﹣2λ，﹣2λ，2λ）（0≤λ≤1），
故 
= + =（1﹣2λ，2﹣2λ，2λ）（0≤λ≤1），
由BF⊥AC，得 =2（1﹣2λ）+2（2﹣2λ）=0，
解得λ= 
，
即 =（﹣ 
， ， 
）， 
= 
+ 
=（1，0，0）+（﹣ ， ， ）=（ ， ， ），
设平面FAD的法向量为 
=（a，b，c），
由 
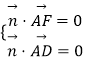，得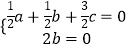 
，∴ 
令c=1，则a=﹣3，则 =（﹣3，0，1），
取平面ADC的法向量 
=（0，0，1），
则二面角F﹣AD﹣C的平面角α满足：
cosα= 
= 
= 
= 
，
故二面角F﹣AD﹣C的余弦值为 ．
【解析】（1）以A为坐标原点，建立如图所示的空间直角坐标系，求出BE，DC的方向向量，根据 =0，可得BE⊥DC；（II）根据BF⊥AC，求出向量 的坐标，进而求出平面FAB和平面ABP的法向量，代入向量夹角公式，可得二面角F﹣AB﹣P的余弦值．
【考点精析】认真审题，首先需要了解直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想)．
