题目内容
设 为双曲线
为双曲线 的两个焦点,点
的两个焦点,点 在双曲线上且
在双曲线上且 ,则
,则 的面积是
的面积是
1
解析试题分析:由题意可得a=1,b=2,c=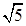 ,得F2(0,
,得F2(0,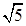 ),F1 (0,-
),F1 (0,-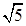 ),
),
又F1F22=20,|PF1-PF2|=4,
由勾股定理可得:
F1F22=PF12+PF22=(PF1-PF2)2+2PF1•PF2=16+2PF1•PF2,
∴PF1•PF2=2,所以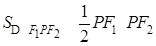 =1.
=1.
故选B..
考点:双曲线的简单性质.

练习册系列答案
相关题目
题目内容
设 为双曲线
为双曲线 的两个焦点,点
的两个焦点,点 在双曲线上且
在双曲线上且 ,则
,则 的面积是
的面积是
1
解析试题分析:由题意可得a=1,b=2,c=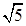 ,得F2(0,
,得F2(0,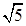 ),F1 (0,-
),F1 (0,-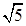 ),
),
又F1F22=20,|PF1-PF2|=4,
由勾股定理可得:
F1F22=PF12+PF22=(PF1-PF2)2+2PF1•PF2=16+2PF1•PF2,
∴PF1•PF2=2,所以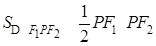 =1.
=1.
故选B..
考点:双曲线的简单性质.
