题目内容
已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点,过点M(4,0)的直线l与抛物线C2分别相交于A,B两点。
(Ⅰ)写出抛物线C2的标准方程;
(Ⅱ)若 ,求直线l的方程;
,求直线l的方程;
(Ⅲ)若坐标原点O关于直线l的对称点P在抛物线C2上,直线l与椭圆C1有公共点,求椭圆C1的长轴长的最小值。
(Ⅰ)写出抛物线C2的标准方程;
(Ⅱ)若
 ,求直线l的方程;
,求直线l的方程;(Ⅲ)若坐标原点O关于直线l的对称点P在抛物线C2上,直线l与椭圆C1有公共点,求椭圆C1的长轴长的最小值。
解:(Ⅰ)由题意,抛物线C2的方程为:y2=4x。
(Ⅱ)设直线AB的方程为:y=k(x-4)(k存在且k≠0),
联立 ,消去x,得ky2-4y-16k=0,
,消去x,得ky2-4y-16k=0,
显然△=16+64k2>0,
设A(x1,y1),B(x2,y2),则 , ①
, ①
y1·y2=-16, ②
又 ,所以,
,所以, ,③
,③
由①②③消去y1,y2,得k2=2,
故直线l的方程为y= x-4
x-4 或y=-x
或y=-x +4
+4 。
。
(Ⅲ)设P(m,n),则OP中点为 ,
,
因为O,P两点关于直线y=k(x-4)对称,
所以, ,
,
即 ,解得:
,解得: ,
,
将其代入抛物线方程,得: ,
,
所以,k2=1,
联立 ,消去y,得
,消去y,得
(b2+a2k2)x2-8k2a2x+16a2k2-a2b2=0,
由△=(-8k2a2)2-4(b2+a2k2)(16a2k2-a2b2)≥0,
得16a2k4-(b2+a2k2)(16k2-b2)≥0,
即a2k2+b2≥16k2,
将k2=1,b2=a2-1代人上式并化简,得 2a2≥17,所以 ,
,
即2a≥ ,
,
因此,椭圆C1长轴长的最小值为 。
。
(Ⅱ)设直线AB的方程为:y=k(x-4)(k存在且k≠0),
联立
 ,消去x,得ky2-4y-16k=0,
,消去x,得ky2-4y-16k=0, 显然△=16+64k2>0,
设A(x1,y1),B(x2,y2),则
 , ①
, ①y1·y2=-16, ②
又
 ,所以,
,所以, ,③
,③由①②③消去y1,y2,得k2=2,
故直线l的方程为y=
 x-4
x-4 或y=-x
或y=-x +4
+4 。
。(Ⅲ)设P(m,n),则OP中点为
 ,
,因为O,P两点关于直线y=k(x-4)对称,
所以,
 ,
,即
 ,解得:
,解得: ,
,将其代入抛物线方程,得:
 ,
,所以,k2=1,
联立
 ,消去y,得
,消去y,得(b2+a2k2)x2-8k2a2x+16a2k2-a2b2=0,
由△=(-8k2a2)2-4(b2+a2k2)(16a2k2-a2b2)≥0,
得16a2k4-(b2+a2k2)(16k2-b2)≥0,
即a2k2+b2≥16k2,
将k2=1,b2=a2-1代人上式并化简,得 2a2≥17,所以
 ,
,即2a≥
 ,
,因此,椭圆C1长轴长的最小值为
 。
。 
练习册系列答案
相关题目
(本小题满分12分)
已知椭圆C1和抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点,从它们每条曲线上至少取两个点,将其坐标记录于下表中:
|
x |
5 |
- |
4 |
|
|
|
y |
2 |
0 |
-4 |
|
- |
(Ⅰ)求C1和C2的方程;
(Ⅱ)过点S(0,- )且斜率为k的动直线l交椭圆C1于A、B两点,在y轴上是否存在定点D,使以线段AB为直径的圆恒过这个点?若存在,求出D的坐标,若不存在,说明理由.
)且斜率为k的动直线l交椭圆C1于A、B两点,在y轴上是否存在定点D,使以线段AB为直径的圆恒过这个点?若存在,求出D的坐标,若不存在,说明理由.






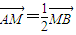 ,求直线l的方程;
,求直线l的方程;