题目内容
14. 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F($\sqrt{3}$,0),长轴长为4.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F($\sqrt{3}$,0),长轴长为4.(Ⅰ)求椭圆C的方程;
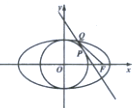
(Ⅱ)设点P是圆x2+y2=b2上第一象限内的任意一点,过P作圆的切线方程与椭圆C在第一象限的交点为Q(x1,y1).求证:|PQ|+|FQ|为定值.
分析 (Ⅰ)根据椭圆的定义与几何性质,求出a、c的值即可;
(Ⅱ)根据点Q在椭圆$\frac{{x}^{2}}{4}$+y2=1上,求出|FQ|的表达式,再根据PQ为圆x2+y2=b2的切线,求出|PQ|的表达式,计算|PQ|+|FQ|即可.
解答 解:(Ⅰ)根据题意得,c=$\sqrt{3}$,2a=4;
∴a=4,
∴b2=a2-c2=1,
∴椭圆的方程为$\frac{{x}^{2}}{4}$+y2=1;…(4分)
(Ⅱ)∵点Q(x1,y1)在椭圆$\frac{{x}^{2}}{4}$+y2=1上,
∴$\frac{{{x}_{1}}^{2}}{4}$+${{y}_{1}}^{2}$=1;
∴|FQ|=$\sqrt{{{(x}_{1}-\sqrt{3})}^{2}{{+y}_{1}}^{2}}$
=$\sqrt{{{(x}_{1}-\sqrt{3})}^{2}+(1-\frac{{{x}_{1}}^{2}}{4})}$
=$\sqrt{{(2-{\frac{\sqrt{3}}{2}x}_{1})}^{2}}$; …(6分)
又∵|x1|≤2,
∴|FQ|=$\sqrt{{(2-{\frac{\sqrt{3}}{2}x}_{1})}^{2}}$=2-$\frac{\sqrt{3}}{2}$x1;…(8分)
又∵PQ为圆x2+y2=b2的切线,
∴|PQ|=$\sqrt{{OQ}^{2}{-OP}^{2}}$
=$\sqrt{{{x}_{1}}^{2}{{+y}_{1}}^{2}-1}$
=$\sqrt{{{x}_{1}}^{2}+1-\frac{{{x}_{1}}^{2}}{4}-1}$
=$\sqrt{{{\frac{3}{4}x}_{1}}^{2}}$
=$\frac{\sqrt{3}}{2}$x1; …(10分)
∴|PQ|+|FQ|=2,和为定值. …(12分)
点评 本题考查了圆的切线方程的应用问题,也考查了椭圆的定义与几何性质的应用问题,考查了直线与圆、直线与椭圆的应用问题,是综合性题目.

 名校课堂系列答案
名校课堂系列答案| A. | {x|x≥-2} | B. | {x|x>-1} | C. | {x|x<-1} | D. | {x|x≤-2} |