题目内容

已知向量a=(2cosα,2sinα),b=(3cosβ,3sinβ),若a与b的夹角为60°,则直线xcosα-ysinα+=0与圆(x-cosβ)2+(y+sinβ)2=1的位置关系是(    )

A.相交             B.相交且过圆心           C.相切               D.相离

提示：由题意,得a·b=|a||b|cosθ,即6cosαcosβ+6sinαsinβ=2×3×cos60°,得cos(α-β)=.

又圆心(cosβ,-sinβ)到直线xcosα-ysinα+=0的距离d=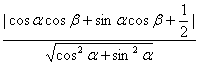

=|cos(α-β)+|=1=r,

所以直线和圆的位置关系是相切,故选C.

答案：C

练习册系列答案
相关题目
已知向量
a
=(2cosα，2sinα)，
b
=(3cosβ，3sinβ)，若向量
a
与
b
的夹角为60°，求cos（α-β）的值．
已知向量
a
=(2cosθ，2sinθ)，θ∈(
π
2
，π)，
b
=(0，-1)，则向量
a
与
b
的夹角为（　　）
已知向量
a
=(2cosθ，1)，
b
=(sinθ+cosθ，1)，- 
π
2
＜θ＜
π
2

（I）若
a
∥
b
，求θ的值
（II）设f（θ）=
a
•
b
，求函数f（θ）的最大值及单调递增区间．
已知向量
a
=(2cosωx，1)，
b
=(sinωx+cosωx，-1)，（ω∈R，ω＞0），设函数f(x)=
a
•
b
(x∈R)，若f（x）的最小正周期为
π
2
．
（1）求ω的值；
（2）求f（x）的单调区间．
（2010•马鞍山模拟）已知向量
a
=(2cos，2sinx)，向量
b
=(
3
cosx，-cosx)，函数f(x)=
a
•
b
-
3
．
（1）求函数f（x）（2）的最小正周期；
（3）求函数f（x）（4）的单调递增区间；
（5）求函数f（x）（6）在区间[
π
12
，
7π
12
]（7）上的值域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网