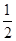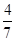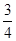题目内容
在区间 上随机取一个数x,
上随机取一个数x, 的值介于0到
的值介于0到 之间的概率为( ).
之间的概率为( ).
A. | B. | C. | D. |
A
解析试题分析:解出关于三角函数的不等式,使得cosx的值介于0到 之间,在所给的范围中,求出符合条件的角的范围,根据几何概型公式用角度之比求解概率.
之间,在所给的范围中,求出符合条件的角的范围,根据几何概型公式用角度之比求解概率.
因为 此区间的长度为
此区间的长度为 ,所以在区间
,所以在区间 上随即取一个数,则cosx的值介于0到
上随即取一个数,则cosx的值介于0到 之间的概率为
之间的概率为 ,故选A.
,故选A.
考点:几何概型概率计算
点评:本题考查的知识点是几何概型,余弦型函数的图象和性质,其中求出cosx的值介于0到 之间时,自变量x的取值范围,是解答的关键.
之间时,自变量x的取值范围,是解答的关键.

练习册系列答案
相关题目
若 是离散型随机变量,
是离散型随机变量,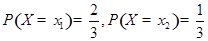 ,且
,且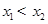 ,又已知
,又已知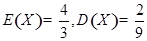 ,则
,则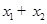 的值为( )
的值为( )
A.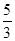 | B.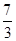 | C. | D.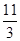 |
从装有5个红球和3个白球的口袋内任取3个球,那么互斥而不对立的事件是( )
| A.至少有一个红球与都是红球 |
| B.至少有一个红球与都是白球 |
| C.至少有一个红球与至少有一个白球 |
| D.恰有一个红球与恰有二个红球 |
已知随机变量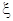 服从正态分布
服从正态分布 且
且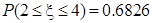 ,则
,则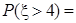 ( )
( )
| A.0.1588 | B.0.1587 | C.0.1586 | D.0.1585 |
甲袋内装有2个红球和3个白球,乙袋内装有1个红球和
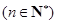 个白球.现分别从甲、乙两袋中各取1个球,若将事件“取出的2个球恰为同色”发生的概率记为
个白球.现分别从甲、乙两袋中各取1个球,若将事件“取出的2个球恰为同色”发生的概率记为 .则以下关于函数
.则以下关于函数
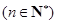 的判断正确的是
的判断正确的是
A. 有最小值,且最小值为 有最小值,且最小值为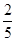 | B. 有最大值,且最大值为 有最大值,且最大值为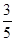 |
C. 有最小值,且最小值为 有最小值,且最小值为 | D. 有最大值,且最大值为 有最大值,且最大值为 |
在区间[0,6]上随机取一个数x,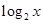 的值介于0到2之间的概率为( )
的值介于0到2之间的概率为( )
A.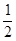 | B.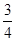 | C.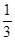 | D.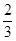 |
若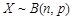 ,且
,且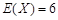 ,
,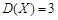 ,则
,则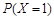 的值为( )
的值为( )
A.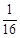 | B.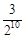 | C.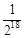 | D.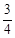 |
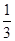
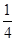
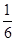
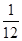
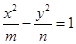 (其中
(其中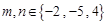 )所表示的圆锥曲线(椭圆、双曲线、抛物线)方程中任取一个,则此方程是焦点在
)所表示的圆锥曲线(椭圆、双曲线、抛物线)方程中任取一个,则此方程是焦点在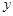 轴上的双曲线方程的概率为( )
轴上的双曲线方程的概率为( )