题目内容
在△ABC中,已知sinB+sinC=sinA(cosB+cosC).
(1)判断△ABC的形状;
(2)若角A所对的边a=1,试求△ABC内切圆半径的取值范围.
(1)判断△ABC的形状;
(2)若角A所对的边a=1,试求△ABC内切圆半径的取值范围.
(1)由已知等式利用正、余弦定理得b+c=a(
+
),…(3分)
整理得(b+c)(b2+c2-a2)=0,
∴b2+c2=a2,
∴△ABC为直角三角形,且∠A=90°.…(6分)
(2)由△ABC为直角三角形,
知内切圆半径r=
=
(sinB+sinC-1)=
(sinB+sinB-1),…(11分)
∵sinB+sinB=
sin(B+
)≤
,
∴0<r≤
.…(14分)
| a2+c2-b2 |
| 2ac |
| a2+b2-c2 |
| 2ab |
整理得(b+c)(b2+c2-a2)=0,
∴b2+c2=a2,
∴△ABC为直角三角形,且∠A=90°.…(6分)
(2)由△ABC为直角三角形,
知内切圆半径r=
| b+c-a |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵sinB+sinB=
| 2 |
| π |
| 4 |
| 2 |
∴0<r≤
| ||
| 2 |

练习册系列答案
相关题目
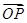 =
=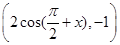 ,
,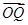 =
=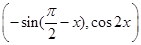 ,定义函数f(x)=
,定义函数f(x)=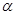 的终边在第一象限,函数
的终边在第一象限,函数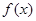 的定义域为
的定义域为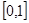 ,且
,且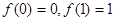 ,当
,当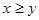 时,有
时,有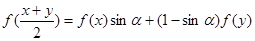 ,则使等式
,则使等式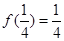 成立的
成立的