Question

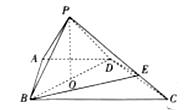
【题目】如图，在四棱锥中，平面，， ，，，，为侧棱上一点.

（Ⅰ）若，求证：平面；

（Ⅱ）求证：平面平面；

（Ⅲ）在侧棱上是否存在点，使得平面？若存在，求出线段的长；若不存在，请说明理由．

Answer 1

【答案】（Ⅰ）详见解析；（Ⅱ）详见解析；（Ⅲ）存在，线段PF长.

【解析】

（Ⅰ）设，连结，由，得，进而证明，即可证明；（Ⅱ）由勾股定理推导，进而证明平面即可求解；（Ⅲ）在平面内作于点，证明平面，进而在直角三角形PAD中求长度

（Ⅰ）设，连结，

由已知，，,得

.

由,得.

在中，由，得.

因为平面，平面，

所以 平面.

（Ⅱ）因为平面，平面，

所以.

由已知得，，，

所以.

所以.

又，所以平面.

因为平面，

所以平面平面.

（Ⅲ）在平面内作于点，

由，，，

得平面.

因为平面，所以.

又，所以平面.

由，，，

得.