题目内容
已知圆x2+y2+x-6y+m=0和直线x+2y-3=0交于P,Q两点,且OP⊥OQ(O为坐标原点),求该圆的圆心坐标及半径.
圆心坐标为![]() ,半径r=
,半径r=![]()
解析:
方法一 将x=3-2y,
代入方程x2+y2+x-6y+m=0,
得5y2-20y+12+m=0.
设P(x1,y1),Q(x2,y2),则y1、y2满足条件:
y1+y2=4,y1y2=![]()
∵OP⊥OQ,∴x1x2+y1y2=0.
而x1=3-2y1,x2=3-2y2.
∴x1x2=9-6(y1+y2)+4y1y2.
∴m=3,此时Δ>0,圆心坐标为![]() ,半径r=
,半径r=![]() .
.
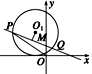
方法二 如图所示,设弦PQ中点为M,
∵O1M⊥PQ,∴![]() .
.
∴O1M的方程为:y-3=2![]() ,
,
即:y=2x+4.
由方程组![]()
解得M的坐标为(-1,2).
则以PQ为直径的圆可设为(x+1)2+(y-2)2=r2.
∵OP⊥OQ,∴点O在以PQ为直径的圆上.
∴(0+1)2+(0-2)2=r2,即r2=5,MQ2=r2.
在Rt△O1MQ中,O1Q2=O1M2+MQ2.
∴![]() (3-2)2+5=
(3-2)2+5=![]()
∴m=3.∴半径为![]() ,圆心为
,圆心为![]() .
.
方法三 设过P、Q的圆系方程为
x2+y2+x-6y+m+![]() (x+2y-3)=0.
(x+2y-3)=0.
由OP⊥OQ知,点O(0,0)在圆上.
∴m-3![]() =0,即m=3
=0,即m=3![]() .
.
∴圆的方程可化为
x2+y2+x-6y+3![]() +
+![]() x+2
x+2![]() y-3
y-3![]() =0
=0
即x2+(1+![]() )x+y2+2(
)x+y2+2(![]() -3)y=0.
-3)y=0.
∴圆心M![]() ,又圆在PQ上.
,又圆在PQ上.
∴-![]() +2(3-
+2(3-![]() )-3=0,
)-3=0,
∴![]() =1,∴m=3.
=1,∴m=3.
∴圆心为![]() ,半径为
,半径为![]() .
.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目