题目内容
已知函数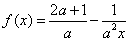 ,常数a>0。
,常数a>0。
(1)设mn>0,证明:函数f(x)在[m,n]上单调递增;
(2)设0<m<n且f(x)的定义域和值域都是[m,n],求n-m的最大值。
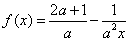 ,常数a>0。
,常数a>0。(1)设mn>0,证明:函数f(x)在[m,n]上单调递增;
(2)设0<m<n且f(x)的定义域和值域都是[m,n],求n-m的最大值。
解:(1)任取 ,且
,且 ,
, ,
,
因为 ,
, ,所以
,所以 >0,
>0,
即 ,故f(x)在[m,n]上单调递增.
,故f(x)在[m,n]上单调递增.
(2)因为f(x)在[m,n]上单调递增,f(x)的定义域、值域都是
 ,
,
即m,n是方程 的两个不等的正根
的两个不等的正根 有两个不等的正根,
有两个不等的正根,
所以 ,
, ,
,
∴ ,
,
∴ 时,n-m取最大值
时,n-m取最大值 。
。
 ,且
,且 ,
, ,
,因为
 ,
, ,所以
,所以 >0,
>0,即
 ,故f(x)在[m,n]上单调递增.
,故f(x)在[m,n]上单调递增. (2)因为f(x)在[m,n]上单调递增,f(x)的定义域、值域都是

 ,
,即m,n是方程
 的两个不等的正根
的两个不等的正根 有两个不等的正根,
有两个不等的正根,所以
 ,
, ,
,∴
 ,
,∴
 时,n-m取最大值
时,n-m取最大值 。
。 
练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
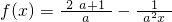 ,常数a>0.
,常数a>0. ,常数a>0.
,常数a>0.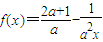 ,常数a>0.
,常数a>0.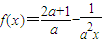 ,常数a>0.
,常数a>0.