Question

如图15，把等腰Rt△ABC沿斜边AB旋转至△ABD的位置，使CD＝AC,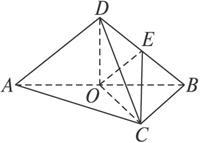

图15

（1）求证：平面ABD⊥平面ABC；

（2）求二面角C-BD-A的余弦值.

Answer 1

（1）证法一:由题设,知AD＝CD＝BD,作DO⊥平面ABC，O为垂足，则OA＝OB＝OC.

∴O是△ABC的外心，即AB的中点.

∴O∈AB，即O∈平面ABD.

∴OD平面ABD.∴平面ABD⊥平面ABC.

证法二:取AB中点O，连接OD、OC,

则有OD⊥AB，OC⊥AB，即∠COD是二面角CABD的平面角.

设AC＝a，则OC＝OD＝a,

又CD＝AD＝AC,∴CD＝a.∴△COD是直角三角形，即∠COD＝90°.

∴二面角是直二面角，即平面ABD⊥平面ABC.

（2）解:取BD的中点E，连接CE、OE、OC,∵△BCD为正三角形，∴CE⊥BD.

又△BOD为等腰直角三角形,∴OE⊥BD.∴∠OEC为二面角C-BD-A的平面角.

同（1）可证OC⊥平面ABD,∴OC⊥OE.∴△COE为直角三角形.

设BC＝a，则CE＝a，OE＝a,∴cos∠OEC＝＝即为所求.