题目内容
凸四边形 中,其中
中,其中 为定点,
为定点, 为动点,
为动点,
满足 .
.
(1)写出 与
与 的关系式;
的关系式;
(2)设 的面积分别为
的面积分别为 和
和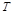 ,求
,求 的最大值。
的最大值。
 中,其中
中,其中 为定点,
为定点, 为动点,
为动点,满足
 .
.(1)写出
 与
与 的关系式;
的关系式;(2)设
 的面积分别为
的面积分别为 和
和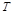 ,求
,求 的最大值。
的最大值。(1) ;(2)
;(2)
 ;(2)
;(2)
试题分析:(1)在三角形BCD和三角形BCD中,利用余弦定理表示出BD2,两者相等表示即可得到cosC与cosA的关系式;
(2)利用三角形面积公式变形出S与T,进而表示出S2+T2,将第一问表示出的cosA代入得到关于cosC的二次函数,利用二次函数性质即可求出S2+T2的最大值.
(1)在⊿PAB中,由余弦定理得:

 3分
3分同理在⊿PQB中
 ∴
∴
∴
 6分
6分(2)
 8分
8分∴


当
 时,
时, 。 12分
。 12分
练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
 ,且
,且 ,求证:
,求证: .
. ),β∈(
),β∈( ,
, ),且5
),且5 sinα+5cosα=8,
sinα+5cosα=8, sinβ+
sinβ+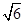 cosβ=2,则cos(α+β)的值为________.
cosβ=2,则cos(α+β)的值为________. +cosα,且α∈(0,
+cosα,且α∈(0, ),则
),则 的值为 .
的值为 . ,
, ,求
,求
 的顶点与原点重合,始边与
的顶点与原点重合,始边与 轴的非负半轴重合,终边在直线
轴的非负半轴重合,终边在直线 上,则
上,则 等于( )
等于( )



 ,
, ,且
,且 ,求
,求 的值.
的值. +
+ i是纯虚数,则tan
i是纯虚数,则tan =( )
=( )

 ,则
,则 .
.