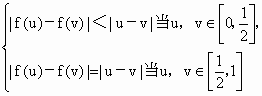题目内容
设y=f(x)是定义在区间(a,b)(b>a)上的函数,若对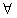 x1、x2∈(a,b),都有|f(x1)-f(x2)|≤|x1-x2|,则称y=f(x)是区间(a,b)上的平缓函数.
x1、x2∈(a,b),都有|f(x1)-f(x2)|≤|x1-x2|,则称y=f(x)是区间(a,b)上的平缓函数.
(1)试证明对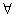 k∈R,f(x)=x2+kx+1都不是区间(-1,1)上的平缓函数;
k∈R,f(x)=x2+kx+1都不是区间(-1,1)上的平缓函数;
(2)若f(x)是定义在实数集R上的、周期为T=2的平缓函数,试证明对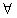 x1、x2∈R,|f(x1)-f(x2)|≤1.
x1、x2∈R,|f(x1)-f(x2)|≤1.
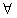 x1、x2∈(a,b),都有|f(x1)-f(x2)|≤|x1-x2|,则称y=f(x)是区间(a,b)上的平缓函数.
x1、x2∈(a,b),都有|f(x1)-f(x2)|≤|x1-x2|,则称y=f(x)是区间(a,b)上的平缓函数. (1)试证明对
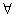 k∈R,f(x)=x2+kx+1都不是区间(-1,1)上的平缓函数;
k∈R,f(x)=x2+kx+1都不是区间(-1,1)上的平缓函数;(2)若f(x)是定义在实数集R上的、周期为T=2的平缓函数,试证明对
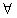 x1、x2∈R,|f(x1)-f(x2)|≤1.
x1、x2∈R,|f(x1)-f(x2)|≤1. 解:(1) ,
,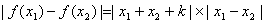 ,
,
若k≥0,则当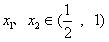 时,
时, ,
,
从而 ;
;
若k<0,则当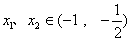 时,
时, ,
,
从而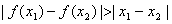 ,
,
所以对任意常数k, 都不是区间(-1,1)上的平缓函数。
都不是区间(-1,1)上的平缓函数。
(2)若 ,
,
①当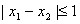 时,
时,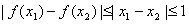 ;
;
②当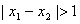 时,不妨设
时,不妨设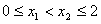 ,根据f(x)的周期性,f(0)=f(2),
,根据f(x)的周期性,f(0)=f(2),
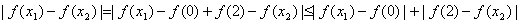 ,
,
 ,
,
所以对 ,都有
,都有 ,
,
对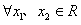 ,根据f(x)的周期性(且T=-2),
,根据f(x)的周期性(且T=-2),
存在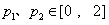 ,使
,使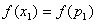 、
、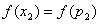 ,
,
从而,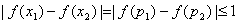 。
。
 ,
,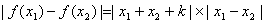 ,
,若k≥0,则当
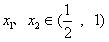 时,
时, ,
,从而
 ;
;若k<0,则当
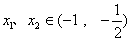 时,
时, ,
,从而
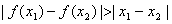 ,
,所以对任意常数k,
 都不是区间(-1,1)上的平缓函数。
都不是区间(-1,1)上的平缓函数。(2)若
 ,
,①当
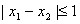 时,
时,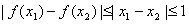 ;
;②当
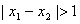 时,不妨设
时,不妨设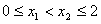 ,根据f(x)的周期性,f(0)=f(2),
,根据f(x)的周期性,f(0)=f(2),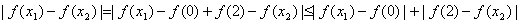 ,
, ,
,所以对
 ,都有
,都有 ,
,对
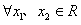 ,根据f(x)的周期性(且T=-2),
,根据f(x)的周期性(且T=-2),存在
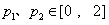 ,使
,使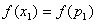 、
、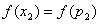 ,
,从而,
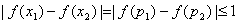 。
。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
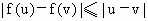 .
.
 .
.