题目内容
已知圆O的方程为:x2+y2=1.
Ⅰ、设过圆O上的一点 作圆O的切线l,求切线l方程;
作圆O的切线l,求切线l方程;
Ⅱ、设圆A:(x-2)2+y2=3与圆O相交于B,C两点,求四边形ABOC的面积.
解:(Ⅰ)由题意,因为点 在圆O:x2+y2=1上
在圆O:x2+y2=1上
所求切线的方程为 ,
,
即3x-4y+5=0
(Ⅱ)因为圆O和圆A的半径分别为OB=1和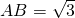 ,又两圆的圆心距OA=2
,又两圆的圆心距OA=2
由勾股定理的逆定理知,OB⊥AB,同理,OC⊥AC
于是,四边形ABOC的面积
分析:(Ⅰ)根据点 在圆O:x2+y2=1上,根据所过点在圆的方程上的切线方程的求法即可得到过P点的切线方程为
在圆O:x2+y2=1上,根据所过点在圆的方程上的切线方程的求法即可得到过P点的切线方程为 ,整理即可得到答案.
,整理即可得到答案.
(Ⅱ)先求出两圆的半径和圆心距,再由勾股定理的逆定理可得到OB⊥AB、OC⊥AC,进而可确定四边形ABOC的面积为 ,整理即可得到答案.
,整理即可得到答案.
点评:本题主要考查过圆上某点的切线方程的求法、两圆之间的关系.考查基础知识的综合运用.
 在圆O:x2+y2=1上
在圆O:x2+y2=1上所求切线的方程为
 ,
,即3x-4y+5=0
(Ⅱ)因为圆O和圆A的半径分别为OB=1和
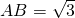 ,又两圆的圆心距OA=2
,又两圆的圆心距OA=2由勾股定理的逆定理知,OB⊥AB,同理,OC⊥AC
于是,四边形ABOC的面积

分析:(Ⅰ)根据点
 在圆O:x2+y2=1上,根据所过点在圆的方程上的切线方程的求法即可得到过P点的切线方程为
在圆O:x2+y2=1上,根据所过点在圆的方程上的切线方程的求法即可得到过P点的切线方程为 ,整理即可得到答案.
,整理即可得到答案.(Ⅱ)先求出两圆的半径和圆心距,再由勾股定理的逆定理可得到OB⊥AB、OC⊥AC,进而可确定四边形ABOC的面积为
 ,整理即可得到答案.
,整理即可得到答案.点评:本题主要考查过圆上某点的切线方程的求法、两圆之间的关系.考查基础知识的综合运用.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目