题目内容
已知函数f(x)=alnx﹣ax﹣3(a∈R)
(1)求f(x)的单调区间;
(2)若函数f(x)的图象在点(2,f)处切线的倾斜角为45°,且对于任意的t∈[1,2],函数![]() 在区间(t,3)上总不为单调函数,求m的取值范围.
在区间(t,3)上总不为单调函数,求m的取值范围.
考点:
利用导数研究函数的单调性;函数的单调性与导数的关系.
专题:
综合题;压轴题.
分析:
(1)先求导数fˊ(x)然后在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,fˊ(x)>0的区间为单调增区间,fˊ(x)<0的区间为单调减区间.
(2)对函数求导,求出函数的单调区间,根据函数的单调区间得到若f(x)在[1,2]上不单调,只要极值点出现在这个区间就可以,得到对于任意的t∈[1,2],g′(t)<0恒成立,从而求m的取值范围.
解答:
解:(1)![]() ,
,
a>0时,f(x)在(0,1]上单调递增,在[1,+∞)单调递减;
a<0时,f(x)在(0,1]上单调递减,在[1,+∞)单调递增;
a=0时,f(x)不是单调函数.
(2)由f′(2)=1得a=﹣2,所以f(x)=﹣2lnx+2x﹣3,则![]() ,
,
故g′(x)=3x2+(m+4)x﹣2
因为g(x)在(t,3)上总不是单调函数,且g′(0)=﹣2,
∴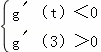 .
.
由题意知:对于任意的t∈[1,2],g′(t)<0恒成立,
综上,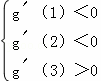
![]() .
.
m的取值范围为:![]() .
.
点评:
本题考查了函数的单调性,利用导数判断函数的单调性的步骤是:(1)确定函数的定义域;(2)求导数fˊ(x);(3)在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0;(4)确定函数的单调区间.若在函数式中含字母系数,往往要分类讨论.

练习册系列答案
相关题目