题目内容
已知x>0,y>0,且 +
+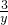 =1,,则
=1,,则 +
+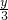 的最小值为
的最小值为
- A.1
- B.2
- C.4
- D.

C
分析:利用“1= +
+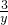 ”代入,将
”代入,将 +
+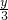 乘以
乘以 +
+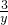 ,即可得到积为定值的和的形式,再用基本不等式即可求出该式的最小值.
,即可得到积为定值的和的形式,再用基本不等式即可求出该式的最小值.
解答:∵x>0,y>0,且 +
+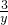 =1,
=1,
∴ +
+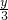 =(
=( +
+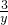 )(
)( +
+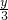 )=2+
)=2+ ,
,
∵

∴当且仅当 =1时,
=1时, +
+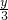 的最小值为4
的最小值为4
故选C
点评:本题结合满足已知等式正数x、y的式子,求该式的最小值,着重考查了用基本不等式求最值的知识点,属于基础题.
分析:利用“1=
 +
+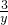 ”代入,将
”代入,将 +
+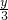 乘以
乘以 +
+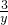 ,即可得到积为定值的和的形式,再用基本不等式即可求出该式的最小值.
,即可得到积为定值的和的形式,再用基本不等式即可求出该式的最小值.解答:∵x>0,y>0,且
 +
+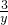 =1,
=1,∴
 +
+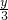 =(
=( +
+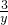 )(
)( +
+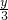 )=2+
)=2+ ,
,∵


∴当且仅当
 =1时,
=1时, +
+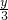 的最小值为4
的最小值为4故选C
点评:本题结合满足已知等式正数x、y的式子,求该式的最小值,着重考查了用基本不等式求最值的知识点,属于基础题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目
(2007
宁夏,7)已知x>0,y>0,x,a,b,y成等差数列,x,c,d,y成等比数列,则 的最小值是
的最小值是
[
]|
A .0 |
B .1 |
C .2 |
D .4 |
 的最小值是( ) A.0 B.1 C.2 D.4
的最小值是( ) A.0 B.1 C.2 D.4