题目内容
如图给定两个长度为1的平面向量
和
，它的夹角为
，点
在以
为圆心的圆弧
上变动，若
，其中
，求
的最大值.
2.
解析试题分析：先建立平面直角坐标系，用坐标表示，由于
模为1，从而得出一个关于
的方程——
，然后再由基本不等式的变形公式
得出的最大值.要注意交待清楚等号成立的条件.
试题解析：以为原点，向量所在方向为
轴正方向，与垂直且向上的方向为
轴正方向，建立如图所示的平面直角坐标系.
设
，由题意得
4分
，
，
，由得，
，
8分
又，当且仅当
时取等号.
所以
12分
即
∴
，当且仅当
时取等号
即
14分
考点：1.向量的坐标表示；2.平面向量的线性运算；3.基本不等式.
练习册系列答案
相关题目
，并求
在
上的投影
，求
的值，并确定此时它们是同向还是反向？
中，
，
为斜边
上靠近顶点
的三等分点.
，求
；
，求
方向上的投影.如果向量
与
共线且方向相反，则
=( )
A． | B． | C．2 | D．0 |
已知
, 
, 且
, 则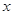
等于 ( )
| A．－1 | B．－9 | C．9 | D．1 |
已知
与
均为单位向量，它们的夹角为
，那么
等于（ ）
A． | B． | C． | D．4 |
如图,在平行四边形
中,
，
，
，则
（ ）(用
，
表示)
A． | B． |
C． | D． |
，若
，则实数
的斜坐标定义为：若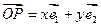
（其中
、
分别为斜坐标系的
轴、
轴正方向上的单位向量，
），则点
．在平面斜坐标系
中，若
，已知点
的斜坐标为
，则点
的距离为 .