题目内容
14.已知α,β∈($\frac{3π}{2}$,2π),满足tan(α+β)-2tanβ=0,则tanα的最小值是( )| A. | $\frac{{3\sqrt{2}}}{4}$ | B. | -$\frac{{\sqrt{2}}}{4}$ | C. | -$\frac{{3\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
分析 利用两角和的正切将tan(α+β)=4tanβ转化,整理为关于tanβ的一元二次方程,利用题意,结合韦达定理即可求得答案
解答 解:∵tan(α+β)-2tanβ=0,
∴tan(α+β)=2tanβ,
∴$\frac{tanα+tanβ}{1-tanαtanβ}$=2tanβ,
∴2tanαtan2β-tanβ+tanα=0,①
∴α,β∈($\frac{3π}{2}$,2π),
∴方程①有两负根,tanα<0,
∴△=1-8tan2α≥0,
∴tan2α≤$\frac{1}{8}$,
∴tanα≥-$\frac{\sqrt{2}}{4}$
∴tanα的最小值是-$\frac{\sqrt{2}}{4}$,
故选:B.
点评 本题考查两角和与差的正切函数,考查一元二次方程中韦达定理的应用,考查转化思想与方程思想,属于中档题

练习册系列答案
相关题目
5.将函数y=sin2x的图象向左平移φ(0<φ<π)个单位后得函数$y=sin({2x-\frac{π}{3}})$的图象,则φ的值为( )
| A. | $\frac{π}{3}$ | B. | $\frac{5π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{6}$ |
2.某校通过随机询问100名性别不同的学生是否能做到“光盘”行动,得到所示联表:
附:K2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$,则下列结论正确的是( )
| 做不到“光盘” | 能做到“光盘” | |
| 男 | 45 | 10 |
| 女 | 30 | 15 |
| P(K2≥k) | 0.10 | 0.05 | 0.01 |
| k | 2.706 | 3.841 | 6.635 |
| A. | 在犯错误的概率不超过1%的前提下,认为“该校学生能否做到‘光盘’与性别无关” | |
| B. | 有99%以上的把握认为“该校学生能否做到‘光盘’与性别有关” | |
| C. | 在犯错误的概率不超过10%的前提下,认为“该校学生能否做到‘光盘’与性别有关” | |
| D. | 有90%以上的把握认为“该校学生能否做到‘光盘’与性别无关” |
3.已知实数x,y满足$\left\{\begin{array}{l}x+y≥1\\{x^2}+{y^2}≤1\end{array}\right.$,则2x+y的取值范围是( )
| A. | [1,2] | B. | [1,+∞) | C. | $(0,\sqrt{5}]$ | D. | $[1,\sqrt{5}]$ |
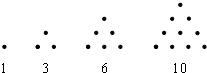 传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数.他们研究过如图的三角形数:
传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数.他们研究过如图的三角形数: