题目内容
若函数f(x)为R上的奇函数,且在定义域上单调递减,又f(sinx-1)>-f(sinx),x∈[0,π],则x的取值范围是
- A.
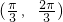
- B.

- C.

- D.

C
分析:本题可根据函数奇函数的性质与函数的单调性将抽象不等式转化为三角不等式,解三角不等式求出x的取值范围,即f(sinx-1)>-f(sinx),f(sinx-1)>f(-sinx),再由函数递减性质得sinx-1<-sinx,解出其在[0,π]上的解集即可选出正确答案.
解答:∵函数f(x)为R上的奇函数,又f(sinx-1)>-f(sinx),
∴f(sinx-1)>-f(sinx),
∴f(sinx-1)>f(-sinx),
又在定义域上单调递减,
∴sinx-1<-sinx,
∴sinx<
又0,π],
∴x∈
故选C.
点评:本题考查正弦函数的单调性,解答本题关键是熟练掌握正弦函数的单调性及函数奇偶性的性质,本题求解两个重点,一个是由单调性将抽象不等式转化为三角不等式,一个是解三角不等式,每一步的求解都要用到一个知识点,知识性较强,有一定的综合性,题后要认真总结一下解题规律,即转化的依据与转化的方式.
分析:本题可根据函数奇函数的性质与函数的单调性将抽象不等式转化为三角不等式,解三角不等式求出x的取值范围,即f(sinx-1)>-f(sinx),f(sinx-1)>f(-sinx),再由函数递减性质得sinx-1<-sinx,解出其在[0,π]上的解集即可选出正确答案.
解答:∵函数f(x)为R上的奇函数,又f(sinx-1)>-f(sinx),
∴f(sinx-1)>-f(sinx),
∴f(sinx-1)>f(-sinx),
又在定义域上单调递减,
∴sinx-1<-sinx,
∴sinx<

又0,π],
∴x∈

故选C.
点评:本题考查正弦函数的单调性,解答本题关键是熟练掌握正弦函数的单调性及函数奇偶性的性质,本题求解两个重点,一个是由单调性将抽象不等式转化为三角不等式,一个是解三角不等式,每一步的求解都要用到一个知识点,知识性较强,有一定的综合性,题后要认真总结一下解题规律,即转化的依据与转化的方式.

练习册系列答案
相关题目
若函数f(x)为R上的奇函数,且在定义域上单调递减,又f(sinx-1)>-f(sinx),x∈[0,π],则x的取值范围是( )
A、(
| ||||
B、[0,
| ||||
C、[0,
| ||||
D、(
|