题目内容
（2013•济宁二模）已知f（x）=
，若|f（x）|≥ax在x∈[-1，1]上恒成立，则实数a的取值范围是（ ）
|
分析：数形结合：分别作出y=|f（x）|、y=ax的图象，由题意即可得到a的取值范围．
解答：解：作出|f（x）|的图象如下图所示：
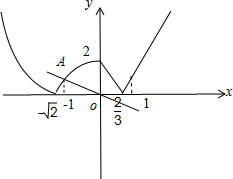因为|f（x）|≥ax在x∈[-1，1]上恒成立，
所以在[-1，1]上|f（x）|的图象应在y=ax图象的上方，
而y=ax表示斜率为a恒过原点的动直线，
由图象知：当直线y=ax从直线OA逆时针旋转到x轴时，其图象在|f（x）|的下方，符合题意
所以有kAO≤a≤0，即-1≤a≤0，
故选A．
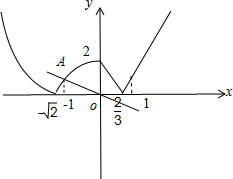因为|f（x）|≥ax在x∈[-1，1]上恒成立，所以在[-1，1]上|f（x）|的图象应在y=ax图象的上方，
而y=ax表示斜率为a恒过原点的动直线，
由图象知：当直线y=ax从直线OA逆时针旋转到x轴时，其图象在|f（x）|的下方，符合题意
所以有kAO≤a≤0，即-1≤a≤0，
故选A．
点评：本题考查函数单调性，考查数形结合思想，考查学生分析解决问题的能力．
练习册系列答案
超能学典应用题题卡系列答案
相关题目