题目内容
椭圆G:![]() (a>b>c)的两个焦点为
(a>b>c)的两个焦点为![]() (-c,0),
(-c,0),![]() (c,0),M是椭圆上一点,且满足
(c,0),M是椭圆上一点,且满足![]() .
.
(1)求离心率e的取值范围;
(2)当离心率e取得最小值时,点N(0,3)到椭圆上的点的最远距离为![]() .①求此时椭圆G的方程.②(只理科作)设斜率为k(k≠0)的直线l与椭圆G相交于不同的两点A、B,Q为AB的中点,问:A、B两点能否关于过点P(0,
.①求此时椭圆G的方程.②(只理科作)设斜率为k(k≠0)的直线l与椭圆G相交于不同的两点A、B,Q为AB的中点,问:A、B两点能否关于过点P(0,![]() ),Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
),Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
答案:
解析:
解析:
|
(1)设点M的坐标为(x,y),则 又由点M在椭圆上,得 ∵ (2)①当离心率e取最小值 设点H(x,y)是椭圆上的一点,则 ②设直线l的方程为y=kx+m,代入 要使A、B两点关于过点P、Q的直线对称,必须 ∵ 由②、③,得 又k≠0,∴ 故当 |

练习册系列答案
 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 ,∴
,∴ ,
,
 已知椭圆G:
已知椭圆G:
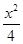 +y2=1,过点(m,0)作圆x2+y2=1的切线l交椭圆G于A、B两点.
+y2=1,过点(m,0)作圆x2+y2=1的切线l交椭圆G于A、B两点.