题目内容
设数列{an}的前项和为Sn,且a1=1,an+1=3Sn(n=1,2,…),则log4S10=( )
分析:通过数列的递推关系式,求出数列的通项公式,然后求出前n项和,计算log4S10即可.
解答:解:因为数列{an}的前项和为Sn,且a1=1,an+1=3Sn(n=1,2,…),所以an+1=4an,
数列是以第二项3为首项4为公比的等比数列,
所以Sn=
=4n-1-1(n>1),所以S10=1+49-1=49.
log4S10=9.
故选A.
数列是以第二项3为首项4为公比的等比数列,
所以Sn=
| 3(1-4n-1) |
| 1-4 |
log4S10=9.
故选A.
点评:本题是中档题,考查数列的递推关系式,注意数列是等比数列的项数,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
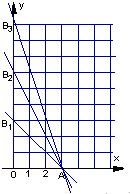 在平面直角坐标系上,设不等式组
在平面直角坐标系上,设不等式组