Question

【题目】已知函数，任取，记函数在区间上的最大值为最小值为记. 则关于函数有如下结论：

①函数为偶函数；

②函数的值域为；

③函数的周期为2；

④函数的单调增区间为.

其中正确的结论有____________.（填上所有正确的结论序号）

Answer 1

【答案】③④.

【解析】

试题因为，其中分别是指函数在区间上的最大值、最小值，注意到函数是最小正周期为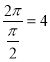的函数，所以在区间的图像与在的图像完全相同，所以，所以，所以函数的一个周期为4，对该函数性质的研究，只须先探究的性质即可.

根据的图像（如下图（1））与性质可知

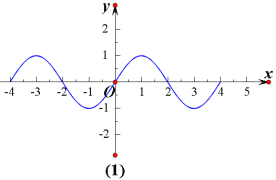
当时，在区间的最小值为，最大值为，此时

当时，在区间的最小值为，最大值为，此时；

当时，在区间的最小值为，最大值为，此时；

当时，在区间的最小值为，最大值为1，此时；

当时，在区间的最小值为，最大值为1，此时；

当时，在区间的最小值为，最大值为，此时

作出的图像，如下图（2）所示

综上可知，该函数没有奇偶性，函数的值域为，从图中可以看到函数的最小正周期为2，函数的单调递增区间为，故只有③④正确.