题目内容
设各项均为正数的数列{an}的前n项和为Sn,已知2a2=a1+a3,数列 是公差为d的等差数列,
是公差为d的等差数列,
(Ⅰ)求数列{an}的通项公式(用n,d表示);
(Ⅱ)设c为实数,对满足m+n=3k且m≠n的任意正整数m,n,k,不等式Sm+Sn>cSk都成立,求证:c的最大值为 。
。
 是公差为d的等差数列,
是公差为d的等差数列,(Ⅰ)求数列{an}的通项公式(用n,d表示);
(Ⅱ)设c为实数,对满足m+n=3k且m≠n的任意正整数m,n,k,不等式Sm+Sn>cSk都成立,求证:c的最大值为
 。
。 解:(Ⅰ)由题设知,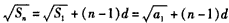 ,
,
则当n≥2时,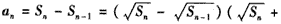
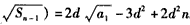 ,
,
由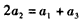 得
得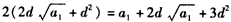 ,
,
解得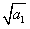 =d,
=d,
故当n≥2时,an=2nd2-d2,
又a1=d2,
所以数列{an}的通项公式为an=(2n-1)d2.
(Ⅱ)由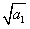 =d及
=d及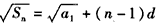 ,
,
得d>0,Sn=d2n2,
于是,对满足题设的m,n,k,m≠n,
有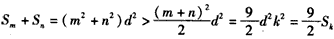 ,
,
所以c的最大值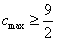 ;
;
另一方面,任取实数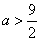 ,
,
设k为偶数,令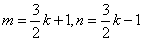 ,则m,n,k符合条件,
,则m,n,k符合条件,
且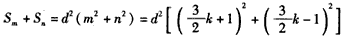
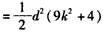 ,
,
于是,只要9k2+4<2ak2,
即当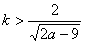 时,就有
时,就有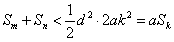 ,
,
所以满足条件的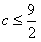 ,从而
,从而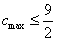 ,
,
因此c的最大值为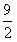 。
。
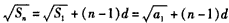 ,
,则当n≥2时,
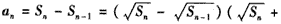
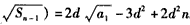 ,
,由
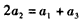 得
得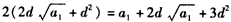 ,
,解得
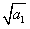 =d,
=d,故当n≥2时,an=2nd2-d2,
又a1=d2,
所以数列{an}的通项公式为an=(2n-1)d2.
(Ⅱ)由
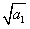 =d及
=d及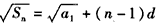 ,
,得d>0,Sn=d2n2,
于是,对满足题设的m,n,k,m≠n,
有
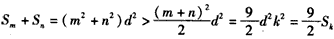 ,
,所以c的最大值
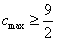 ;
;另一方面,任取实数
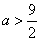 ,
,设k为偶数,令
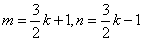 ,则m,n,k符合条件,
,则m,n,k符合条件,且
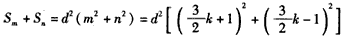
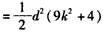 ,
,于是,只要9k2+4<2ak2,
即当
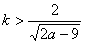 时,就有
时,就有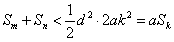 ,
,所以满足条件的
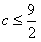 ,从而
,从而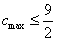 ,
,因此c的最大值为
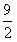 。
。 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目