题目内容
2.已知四棱锥S-ABCD的所有顶点都在半径为2的球O的球面上,四边形ABCD是边长为2的正方形,SC为球O的直径,则此棱锥的体积为( )| A. | $\frac{4\sqrt{2}}{3}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{8\sqrt{2}}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
分析 根据题意得出空间几何体的直观图,利用圆的几何知识得出Rt△SBC,Rt△SDC,Rt△SAC,利用边长根据勾股定理得出△ABS,△ADS,为直角三角形,可得SA⊥平面ABC,即可求棱锥的体积.
解答 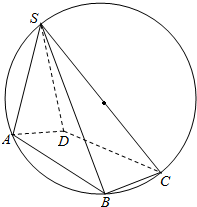 解:根据题意得出:
解:根据题意得出:
AC=2$\sqrt{2}$,SC=4,AB=BC=DC=DA=2
根据圆的几何知识得出Rt△SBC,Rt△SDC,Rt△SAC,
∴可知SD=SB=2$\sqrt{3}$,SA=2$\sqrt{2}$,
根据勾股定理得出△ABS,△ADS,为直角三角形.
∴SA⊥AC,SA⊥AB,
∵AC∩AB=A,
∴SA⊥平面ABC,
∴棱锥的体积为$\frac{1}{3}×2×2×2\sqrt{2}$=$\frac{8\sqrt{2}}{3}$,
故选:C.
点评 本题考查了球的内接几何体的问题,充分利用圆的知识得出直线,平面的位置关系,从而利用公式求解即可.

练习册系列答案
相关题目
12.有3个学习兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
13.定义在R上的偶函数f(x)满足f(x+1)=-f(x),且在[-5,-4]上是减函数,α、β是锐角三角形的两个内角,则( )
| A. | f(sinα)>f(cosβ) | B. | f(sinα)>f(sinβ) | C. | f(sinα)<f(cosβ) | D. | f(cosα)>f(cosβ) |
17.已知变量x、y满足约束条件:$\left\{\begin{array}{l}{y≥x}\\{x+2y≤2}\\{x≥-2}\end{array}\right.$,则z=x-3y的最小值是( )
| A. | -$\frac{4}{3}$ | B. | 4 | C. | -4 | D. | -8 |
14.在一项吃零食与性别的调查中,运用2×2列联表进行独立性检验得到K2≈2.521,那么判断吃零食和性别有关的这种判断的出错率为( )
| A. | 1% | B. | 99% | C. | 15% | D. | 90% |
10.过椭圆9x2+y2=1的一个焦点F1的直线与椭圆交于A,B两点,则A与B和椭圆的另一个焦点F2构成的三角形ABF2的周长是( )
| A. | $\frac{4}{3}$ | B. | 4 | C. | 8 | D. | 2$\sqrt{2}$ |