题目内容
定义:关于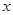 的不等式
的不等式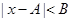 的解集叫
的解集叫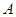 的
的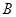 邻域.已知
邻域.已知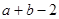 的
的 邻域为区间
邻域为区间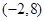 ,其中
,其中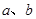 分别为椭圆
分别为椭圆 的长半轴和短半轴.若此椭圆的一焦点与抛物线
的长半轴和短半轴.若此椭圆的一焦点与抛物线 的焦点重合,则椭圆的方程为( . )
的焦点重合,则椭圆的方程为( . )
A.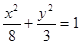 | B.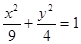 |
C.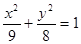 | D.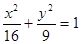 |
B
解析试题分析:由邻域的定义,a,b满足|x-(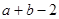 )|<
)|< ,-2<x<2(
,-2<x<2( )-2,而已知
)-2,而已知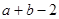 的
的 邻域为区间
邻域为区间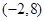 ,所以2(
,所以2( )-2=8,
)-2=8, =5.又此椭圆的一焦点与抛物线
=5.又此椭圆的一焦点与抛物线 的焦点(
的焦点( ,0)重合,即c=
,0)重合,即c= ,结合
,结合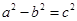 得,a-b=1,解得a=3,b=2,所求椭圆方程为
得,a-b=1,解得a=3,b=2,所求椭圆方程为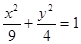 ,故选B。
,故选B。
考点:本题主要考查绝对值不等式解法,椭圆的标准方程及几何性质,抛物线的几何性质。
点评:新定义问题,此类问题,首要的是理解题意。不难看到,理解题意后,主要是解方程组。利用圆锥曲线的几何性质解题。

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
椭圆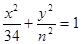 和双曲线
和双曲线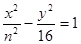 有相同的焦点,则实数
有相同的焦点,则实数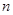 的值是 ( )
的值是 ( )
A.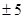 | B.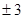 | C.5 | D.9 |
抛物线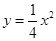 的焦点坐标是( )
的焦点坐标是( )
A.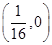 | B.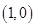 | C.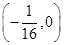 | D.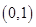 |
方程 的曲线是( )
的曲线是( )
| A.一个点 | B.一条直线 | C.两条直线 | D.一个点和一条直线 |
从抛物线 上任意一点
上任意一点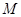 向圆
向圆 作切线
作切线 ,则切线长
,则切线长 的最小值为
的最小值为
A.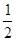 | B.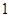 | C. | D.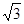 |
 的右顶点A作斜率为一1的直线,该直线与双曲线的两条渐近线的交点分别为B,C,若A,B,C三点的横坐标成等比数列,则双曲线的离心率为
的右顶点A作斜率为一1的直线,该直线与双曲线的两条渐近线的交点分别为B,C,若A,B,C三点的横坐标成等比数列,则双曲线的离心率为




 与抛物线
与抛物线 相交于
相交于 两点,F为抛物线的焦点,若
两点,F为抛物线的焦点,若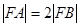 ,则k的值为( )。
,则k的值为( )。



 的一条渐近线与圆
的一条渐近线与圆 有公共点,则双曲线的离心率的取值范围是( )
有公共点,则双曲线的离心率的取值范围是( )




 与抛物线
与抛物线 相交于
相交于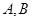 两点,F为抛物线的焦点,若
两点,F为抛物线的焦点,若 ,则k的值为( )。
,则k的值为( )。


