题目内容
已知直线l:y=x+b和圆C:x2+y2-2x-1=0,则“b=1”是“直线l与圆C相切”的
- A.充要条件
- B.充分不必要条件
- C.必要不充分条件
- D.既不充分也不必要条件
B
分析:根据直线与圆相切的性质可知,当直线与圆相切时,利用圆心到直线的距离等于半径可求b,从而可判断
解答:若b=1,直线方程为x-y+1=0,圆(x-1)2+y2=2的圆心(1,0),半径r=
此时圆心(1,0)到直线x-y+1=0的距离d=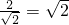 =r
=r
∴直线l与圆C相切
若直线l与圆C相切,则圆心(1,0)到直线x-y+b=0的距离d=
∴b=1或b=-3
∴b=1”是“直线l与圆C相切”的充分不必要条件
故选B
点评:本题以充分条件与必要条件的判断为载体,主要考查了直线与圆相切的性质的应用.
分析:根据直线与圆相切的性质可知,当直线与圆相切时,利用圆心到直线的距离等于半径可求b,从而可判断
解答:若b=1,直线方程为x-y+1=0,圆(x-1)2+y2=2的圆心(1,0),半径r=

此时圆心(1,0)到直线x-y+1=0的距离d=
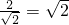 =r
=r∴直线l与圆C相切
若直线l与圆C相切,则圆心(1,0)到直线x-y+b=0的距离d=

∴b=1或b=-3
∴b=1”是“直线l与圆C相切”的充分不必要条件
故选B
点评:本题以充分条件与必要条件的判断为载体,主要考查了直线与圆相切的性质的应用.

练习册系列答案
相关题目